/Szkoła średnia/Liczby/Potęgi i pierwiastki/Udowodnij...

Zadanie nr 6308091

Wykaż, że 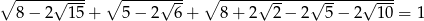∘ -----√---- ∘ -----√--- ∘ -----√------√------√---- 8− 2 15+ 5 − 2 6 + 8+ 2 2− 2 5− 2 10 = 1 .

Wersja PDF

Rozwiązanie

Ostatni pierwiastek wygląda najgorzej, więc zostawmy go sobie na koniec i zajmijmy się najpierw dwoma pierwszymi pierwiastkami.

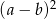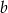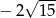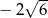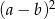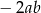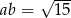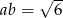Domyślamy się, że wyrażenie pod każdym z tych pierwiastków jest pełnym kwadratem postaci (a − b)2 - pozostaje zgadnąć ile są równe a i b . Za wskazówkę należy przyjąć składniki √ --- − 2 15 i √ -- − 2 6 . Skoro spodziewamy się wyrażenia postaci 2 (a − b) składniki te muszą być równe − 2ab . Zatem √ --- ab = 15 i √ -- ab = 6 odpowiednio. Teraz już łatwo, np. w przypadku pierwszego pierwiastka spodziewamy się zatem jednej z możliwości

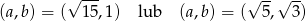
√ --- √ --√ -- (a,b) = ( 15 ,1 ) lub (a ,b ) = ( 5, 3)

(odwrotne pary nie dają nic nowego, bo 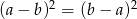2 2 (a− b) = (b − a) ). Łatwo sprawdzić, że prawidłowa jest druga konfiguracja:

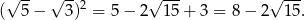
√ -- √ -- √ --- √ --- ( 5 − 3)2 = 5 − 2 1 5+ 3 = 8− 2 15.

Podobnie rozszyfrowujemy drugi pierwiastek

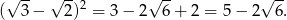
√ -- √ -- √ -- √ -- ( 3 − 2)2 = 3 − 2 6+ 2 = 5− 2 6.

Daną równość możemy więc przekształcić następująco:

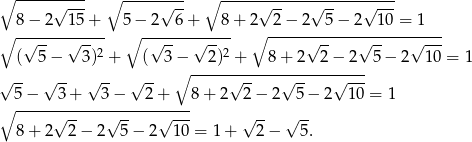
∘ -----√---- ∘ ------√--- ∘ -----√------√------√---- 8 − 2 15 + 5 − 2 6+ 8+ 2 2 − 2 5 − 2 10 = 1 ∘ -√-----√----- ∘ -√-----√----- ∘ -----√-------√------√---- ( 5 − 3)2 + ( 3 − 2)2 + 8 + 2 2 − 2 5− 2 10 = 1 ∘ ------------------------ √ -- √ -- √ -- √ -- √ -- √ -- √ --- ∘ 5−----3+----3−----2+----8+ 2 2 − 2 5 − 2 10 = 1 √ -- √ -- √ --- √ -- √ -- 8 + 2 2 − 2 5 − 2 10 = 1+ 2− 5.

Ponieważ obie strony powyższej równości są dodatnie, wystarczy wykazać, że

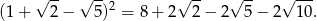
√ -- √ --2 √ -- √ -- √ --- (1 + 2 − 5) = 8 + 2 2− 2 5− 2 10.

Skorzystamy ze wzoru

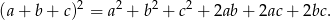
2 2 2 2 (a + b + c) = a + b + c + 2ab+ 2ac+ 2bc.

Liczymy

√ -- √ --2 √ -- √ -- √ --- L = (1+ 2− 5) = 1 + 2 +-5 + 2 -2 − 2 -5-− 2 10 = 8 + 2√ 2 − 2√ 5 − 2√ 1 0 = P.
Wersja PDF