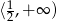/Szkoła średnia/Funkcje/Liniowa

Zadanie nr 1076701

Dana jest funkcja liniowa 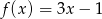f (x) = 3x − 1 .

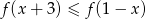  • Rozwiąż nierówność f(x + 3) ≤ f (1− x) .
  • Podaj maksymalne przedziały monotoniczności funkcji f(x− x2) .
Wersja PDF

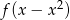Rozwiązanie

  • Liczymy
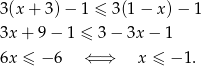
    3(x + 3) − 1 ≤ 3(1 − x) − 1 3x + 9 − 1 ≤ 3 − 3x − 1 6x ≤ − 6 ⇐ ⇒ x ≤ − 1.

     
    Odpowiedź: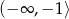 (− ∞ ,− 1⟩

  • Liczymy
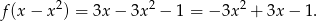
    2 2 2 f(x − x ) = 3x− 3x − 1 = − 3x + 3x − 1.

    Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół, więc jest rosnąca na lewo i malejąca na prawo od wierzchołka. Sprawdźmy jaka jest pierwsza współrzędna wierzchołka.

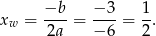
    −b-- −3-- 1- xw = 2a = −6 = 2 .

     
    Odpowiedź: Rosnąca na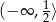 1 (− ∞ ,2⟩ , malejąca na ⟨1 ,+ ∞ ) 2

Wersja PDF