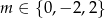Zadanie nr 1819117

Dla jakich wartości parametru 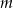funkcja 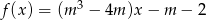3 f(x ) = (m − 4m )x − m − 2 jest:

Rozwiązanie

Funkcja liniowa jest malejąca, gdy współczynnik kierunkowy jest ujemy.
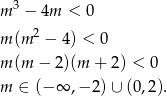
$m 3 − 4m < 0 2 m (m − 4 ) < 0 m (m − 2)(m + 2) < 0 m ∈ (− ∞ ,− 2)∪ (0,2).$

Odpowiedź: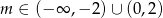
Sposób I

Sprawdźmy kiedy .

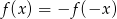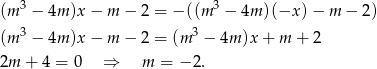
$3 3 (m − 4m )x − m − 2 = − ((m − 4m )(−x )− m − 2) (m 3 − 4m )x − m − 2 = (m 3 − 4m )x + m + 2 2m + 4 = 0 ⇒ m = − 2.$

Sposób II

Ponieważ wykres funkcji nieparzystej jest symetryczny względem początku układu współrzędnych, funkcja liniowa jest nieparzysta dokładnie wtedy, gdy jej wykres przechodzi przez punkt 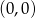, czyli dla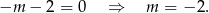

$−m − 2 = 0 ⇒ m = − 2.$

Odpowiedź: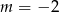
Sposób I

Sprawdźmy kiedy .

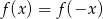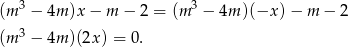
$3 3 (m − 4m )x − m − 2 = (m − 4m )(−x )− m − 2 (m3 − 4m )(2x ) = 0.$

Równość ta ma zachodzić dla dowolnego , zatem

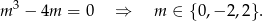
$m3 − 4m = 0 ⇒ m ∈ { 0,− 2,2}.$

Sposób II

Ponieważ wykres funkcji parzystej jest symetryczny względem osi , funkcja liniowa jest parzysta dokładnie wtedy, gdy jest stała, czyli dla

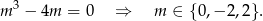
$3 m − 4m = 0 ⇒ m ∈ { 0,− 2,2}.$

Odpowiedź: