/Szkoła średnia/Funkcje/Liniowa

Zadanie nr 8017336

Wiadomo, że funkcja liniowa 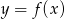y = f(x) przyjmuje wartości dodatnie wtedy i tylko wtedy, gdy 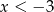x < − 3 . Ponadto, 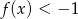f (x) < − 1 wtedy i tylko wtedy, gdy 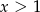x > 1 . Wyznacz wzór funkcji f .

Wersja PDF

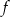Rozwiązanie

Myślimy o prostej będącej wykresem funkcji 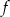f . Wiemy, że prosta ta znajduje się powyżej osi 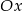Ox dokładnie na zbiorze 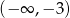(− ∞ ,−3 ) . To oznacza, że prosta ta musi przecinać 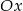Ox w punkcie (− 3,0) .

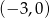Podobnie wykorzystujemy drugą informację – skoro wykres funkcji ma być poniżej prostej 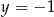y = − 1 dokładnie na zbiorze 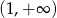(1,+ ∞ ) , wykres funkcji musi przechodzić przez punkt 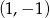(1,− 1) . Musimy więc napisać równanie prostej przechodzącej przez punkty 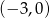(− 3,0 ) i (1 ,−1 ) .

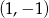Szukamy prostej w postaci 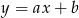y = ax + b . Podstawiając współrzędne powyższych punktów mamy

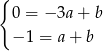
{ 0 = − 3a + b − 1 = a+ b

Odejmując od drugiego równania pierwsze (żeby zredukować 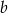b ) mamy 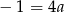− 1 = 4a , czyli 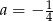a = − 1 4 . Wówczas

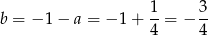
1- 3- b = − 1− a = − 1 + 4 = − 4

i szukana prosta to 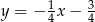y = − 14x − 34 . Na koniec obrazek.

PIC

 
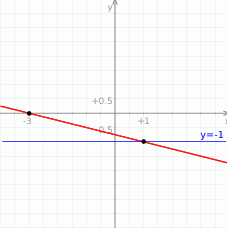
Odpowiedź: y = − 14x− 34

Wersja PDF