/Konkursy/Zadania/Liczby

Zadanie nr 1284783

Dodaj do ulubionych
Dodaj do rozwiązanych

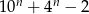Udowodnij, że dla każdej liczby naturalnej n , liczba n n 10 + 4 − 2 jest liczbą podzielną przez 3.

Rozwiązanie

Sposób I

Skorzystamy ze wzoru

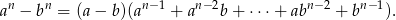
n n n− 1 n−2 n−2 n− 1 a − b = (a − b)(a + a b + ⋅⋅⋅+ ab + b ).

Przekształćmy podane wyrażenie

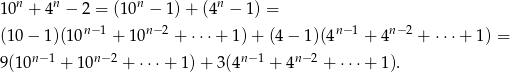
n n n n 10 + 4 − 2 = (10 − 1)+ (4 − 1) = (10 − 1)(10n −1 + 10n−2 + ⋅⋅⋅ + 1)+ (4− 1)(4n−1 + 4n− 2 + ⋅ ⋅⋅+ 1) = n− 1 n−2 n−1 n− 2 9(10 + 10 + ⋅⋅⋅+ 1)+ 3(4 + 4 + ⋅⋅⋅+ 1).

Widać, że liczba ta jest podzielna przez 3.

Sposób II

Ponieważ 10 daje resztę 1 z dzielenia przez 3 (tzn. 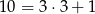10 = 3 ⋅3+ 1 ), to taką samą resztę daje dowolna potęga 10 (reszta potęgi liczby to potęga reszty). Podobnie 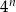n 4 daje resztę 1 z dzielenia przez 3. Zatem całe wyrażenie daje resztę 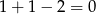1 + 1 − 2 = 0 . Całe to rozumowanie wygodnie zapisuje się przy pomocy kongruencji

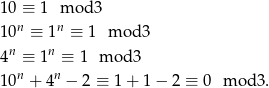
10 ≡ 1 m od3 10n ≡ 1n ≡ 1 m od 3 n n 4 ≡ 1 ≡ 1 m od 3 10n + 4n − 2 ≡ 1 + 1 − 2 ≡ 0 m od 3.

Korzystaliśmy z tego, że kongruencje można potęgować i dodawać stronami.

Wersja PDF