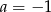Zadanie nr 2557861
Wykaż, że liczba 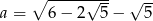 jest całkowita.
jest całkowita.
Rozwiązanie
Sposób I
Liczymy
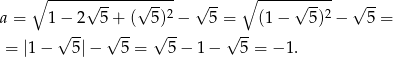
Sposób II
Liczymy
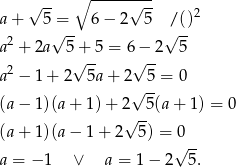
Aby wykluczyć drugą możliwość wystarczy sprawdzić, że wtedy 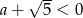 co nie jest możliwe (pierwsza równość powyżej).
co nie jest możliwe (pierwsza równość powyżej).
Odpowiedź: 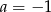
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że liczba 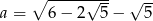 jest całkowita.
jest całkowita.
Sposób I
Liczymy
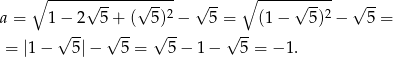
Sposób II
Liczymy
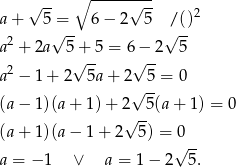
Aby wykluczyć drugą możliwość wystarczy sprawdzić, że wtedy 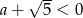 co nie jest możliwe (pierwsza równość powyżej).
co nie jest możliwe (pierwsza równość powyżej).
Odpowiedź: