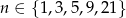Zadanie nr 3417192
Znajdź wszystkie liczby całkowite dodatnie 
, dla których liczba 
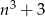jest podzielna przez 
.
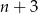Rozwiązanie
Musimy sprawdzić kiedy ułamek
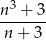
jest liczbą naturalną. Przekształcamy go tak, aby w liczniku nie było 
(dzielimy licznik przez mianownik grupując wyrazy).
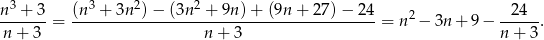
Widzimy więc, że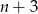 
musi dzielić 24, czyli 
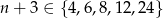. Zatem 
.
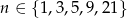Rozkład licznika mogliśmy też zrobić trochę sprytniej korzystając ze wzoru
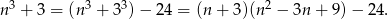
Odpowiedź: 
