/Konkursy/Zadania/Liczby

Zadanie nr 8089833

Dodaj do ulubionych
Dodaj do rozwiązanych

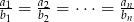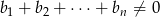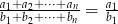Wykaż, że jeśli a1 a2 an b1 = b2 = ⋅⋅ ⋅ = bn i b 1 + b2 + ⋅⋅⋅ + bn ⁄= 0 , to a1+a2+⋅⋅⋅+an a1 b1+b2+⋅⋅⋅+bn = b1 .

Rozwiązanie

Sposób I

Podane warunki możemy zapisać w postaci

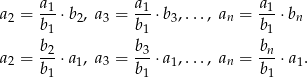
a-1 a1- a1- a2 = b ⋅b2, a3 = b ⋅b3,..., an = b ⋅bn 1 1 1 a2 = b2-⋅a1, a3 = b3-⋅a1,..., an = bn-⋅a1. b1 b1 b 1

Teraz możemy przekształcić lewą stronę żądanej równości.

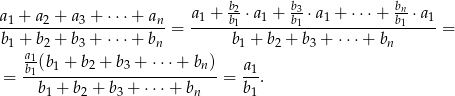
b b a1 + a2 + a3 + ⋅⋅⋅+ an a1 + b21 ⋅ a1 + 3b1-⋅a1 + ⋅⋅⋅+ bbn1 ⋅a1 -----------------------= ----------------------------------= b1 +a b2 + b3 + ⋅⋅⋅+ bn b1 + b2 + b3 + ⋅⋅⋅+ bn b11(b1-+-b2 +-b3 +-⋅⋅⋅+-bn-) a1- = b + b + b + ⋅⋅⋅+ b = b . 1 2 3 n 1

Sposób II

Wymnażamy podany warunek na krzyż.

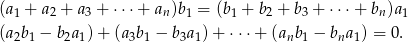
(a + a + a + ⋅ ⋅⋅+ a )b = (b + b + b + ⋅⋅⋅+ b )a 1 2 3 n 1 1 2 3 n 1 (a2b1 − b2a1)+ (a3b1 − b3a1)+ ⋅ ⋅⋅+ (anb1 − bna1) = 0.

Na mocy założenia, każdy z nawiasów jest równy 0, co dowodzi żądanej równości.

Wersja PDF