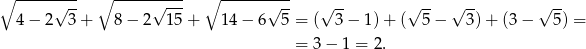Zadanie nr 9529884
Wykaż, że
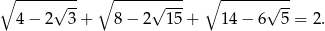
Rozwiązanie
Próbujemy pod każdym z pierwiastków dostrzec wzór skróconego mnożenia
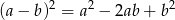
na kwadrat różnicy.
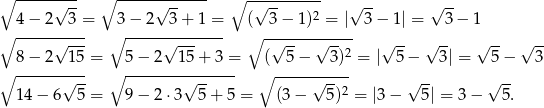
Stąd
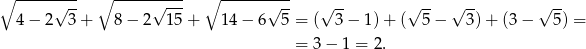
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że
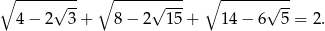
Próbujemy pod każdym z pierwiastków dostrzec wzór skróconego mnożenia
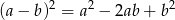
na kwadrat różnicy.
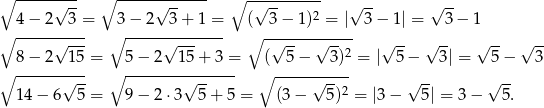
Stąd