Zadanie nr 6271544
Wykaż, że liczba  jest dla dowolnej liczby naturalnej
jest dla dowolnej liczby naturalnej  kwadratem liczby całkowitej.
kwadratem liczby całkowitej.
Rozwiązanie
Przekształcamy wzór
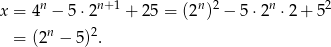
Zatem dla każdej liczby naturalnej  liczba
liczba  jest kwadratem liczby
jest kwadratem liczby 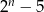 która jest oczywiście liczbą całkowitą.
która jest oczywiście liczbą całkowitą.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że liczba  jest dla dowolnej liczby naturalnej
jest dla dowolnej liczby naturalnej  kwadratem liczby całkowitej.
kwadratem liczby całkowitej.
Przekształcamy wzór
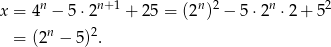
Zatem dla każdej liczby naturalnej  liczba
liczba  jest kwadratem liczby
jest kwadratem liczby 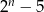 która jest oczywiście liczbą całkowitą.
która jest oczywiście liczbą całkowitą.
