/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 3598115

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykazać, że odcinki łączące kolejne środki kwadratów zbudowanych na bokach równoległoboku tworzą także kwadrat.

PIC

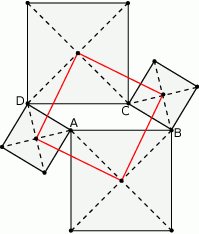
Rozwiązanie

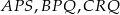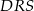Rozpoczniemy od obserwacji, że cztery trójkąty AP S ,BP Q ,CRQ i DRS są przystające.

PIC

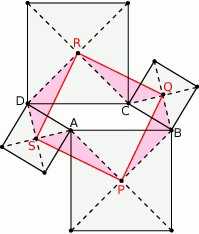
Rzeczywiście, mają dwie pary równych boków

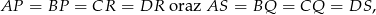
AP = BP = CR = DR oraz AS = BQ = CQ = DS ,

oraz w każdym z tych trójkątów boki te spotykają się pod tym samym kątem

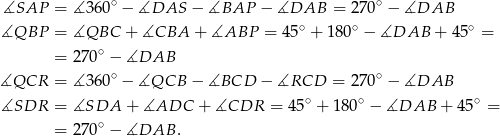
∡SAP = ∡3 60∘ − ∡DAS − ∡BAP − ∡DAB = 270∘ − ∡DAB ∡QBP = ∡QBC + ∡CBA + ∡ABP = 4 5∘ + 1 80∘ − ∡DAB + 4 5∘ = ∘ = 270 − ∡DAB ∡QCR = ∡3 60∘ − ∡QCB − ∡BCD − ∡RCD = 270∘ − ∡DAB ∘ ∘ ∘ ∡SDR = ∡SDA + ∡ADC + ∡CDR = 45 + 18 0 − ∡DAB + 45 = = 270∘ − ∡DAB .

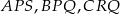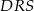Z przystawania trójkątów AP S,BP Q ,CRQ i DRS otrzymujemy

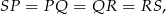
SP = PQ = QR = RS ,

czyli czworokąt 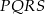P QRS jest rombem.

Ponadto,

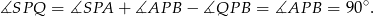
∡SP Q = ∡SPA + ∡AP B − ∡QP B = ∡AP B = 90∘.

Jest to więc kwadrat.

Wersja PDF