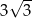/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 4768385

Dłuższa przekątna równoległoboku o kącie ostrym 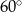∘ 60 ma długość 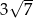√ -- 3 7 . Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

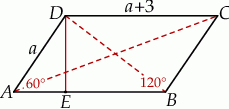
Napiszemy twierdzenie cosinusów w trójkącie 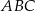ABC i to pozwoli nam obliczyć a .

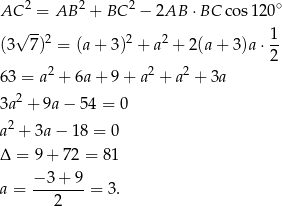
AC 2 = AB 2 + BC 2 − 2AB ⋅BC co s120∘ √ -- 1 (3 7)2 = (a+ 3)2 + a2 + 2 (a+ 3 )a⋅-- 2 6 3 = a2 + 6a+ 9+ a2 + a2 + 3a 2 3a + 9a − 5 4 = 0 a 2 + 3a − 18 = 0 Δ = 9 + 72 = 81 −-3+--9 a = 2 = 3.

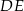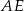Możemy teraz obliczyć długości odcinków DE i AE z trójkąta AED .

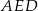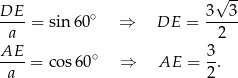
√ -- DE ∘ 3 3 -a--= sin 60 ⇒ DE = --2-- AE--= co s60∘ ⇒ AE = 3. a 2

Pozostało policzyć pole i drugą przekątną.

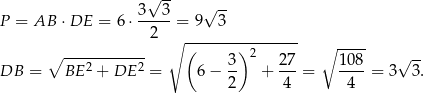
√ -- √ -- P = AB ⋅DE = 6⋅ 3--3-= 9 3 2 ∘ ---------------- ∘ ------------ ( )2 ∘ ---- √ -- DB = BE 2 + DE 2 = 6 − 3- + 27-= 1-08 = 3 3. 2 4 4

 
Odpowiedź: Pole: 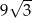√ -- 9 3 , przekątna: √ -- 3 3

Wersja PDF