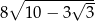/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 5627148

Kąt ostry równoległoboku ma miarę 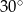∘ 30 . Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.

Wersja PDF

Rozwiązanie

Jak to w zadaniach geometrycznych najważniejszy jest rysunek.

PIC

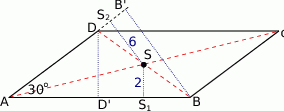
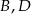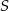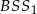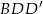Oznaczmy rzuty punktów B,D i S jak na rysunku. Ponieważ przekątne równoległoboku dzielą się na połowy, trójkąty BSS 1 i BDD ′ są podobne w skali 1:2. Daje to nam

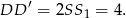
DD ′ = 2SS = 4. 1

Podobnie wyliczamy drugą wysokość (patrzymy na trójkąty podobne 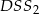DSS 2 i ′ DBB )

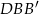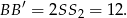
′ BB = 2SS 2 = 12.

Aby obliczyć pole, musimy znać długość podstawy. Aby ją wyliczyć patrzymy na trójkąt 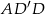′ AD D jest on prostokątny i 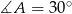∘ ∡A = 30 . Mamy stąd

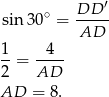
′ sin 30∘ = DD--- AD 1 4 --= ---- 2 AD AD = 8.

Podobnie wyliczamy

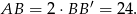
AB = 2 ⋅BB ′ = 24.

Możemy więc wyliczyć pole równoległoboku

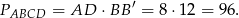
′ PABCD = AD ⋅ BB = 8 ⋅12 = 96.

Długość krótszej przekątnej możemy wyliczyć stosując twierdzenie cosinusów w trójkącie ABD .

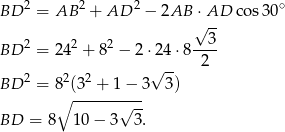
2 2 2 ∘ BD = AB + AD − 2AB ⋅√ AD cos30 3 BD 2 = 242 + 82 − 2⋅ 24⋅8 ---- √ -- 2 BD 2 = 82(32 + 1− 3 3) ∘ -------√--- BD = 8 1 0− 3 3.

 
Odpowiedź: Pole: 96, przekątna: ---------- ∘ √ -- 8 10− 3 3

Wersja PDF