/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 5982399

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole równoległoboku jest równe 24. Stosunek jego wysokości jest równy 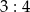3 : 4 . Długości boków wyrażają się liczbami naturalnymi, a długość każdej z wysokości jest mniejsza od 5 i większa od 2. Oblicz długości boków równoległoboku.

Rozwiązanie

Zaczynamy od rysunku

PIC

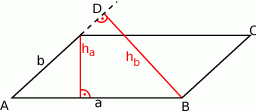
Skoro wysokości mają długość mniejszą od 5 i większą od 2, a pole jest równe 24 to

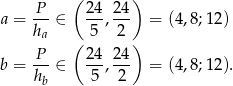
( ) a = P--∈ 24, 2-4 = (4,8;12) ha 5 2 ( ) b = P--∈ 24, 2-4 = (4,8;12). hb 5 2

Zatem długości boków równoległoboku są liczbami naturalnymi z przedziału 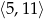⟨5,11 ⟩ . Wiemy ponadto, że

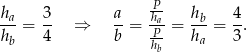
ha 3 a Ph- hb 4 ---= -- ⇒ --= -Pa= ---= -. hb 4 b hb ha 3

Liczby 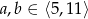a,b ∈ ⟨5,11 ⟩ mają być całkowite i takie, że 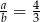ab = 43 – jedyna możliwość to 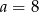a = 8 i b = 6 .  
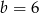Odpowiedź: 6 i 8

Wersja PDF