Zadanie nr 7250531
W równoległoboku o obwodzie równym 144, wysokości 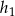 i
i 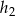 spełniają warunek
spełniają warunek 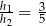 . Oblicz długości boków tego równoległoboku.
. Oblicz długości boków tego równoległoboku.
Rozwiązanie
Zacznijmy od schematycznego rysunku i oznaczmy podstawy na które są opuszczone wysokości 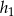 i
i 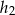 przez
przez  i
i 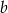 odpowiednio.
odpowiednio.
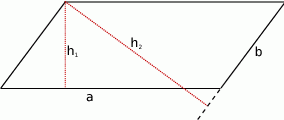
Ze wzoru na pole równoległoboku:
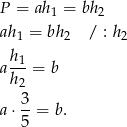
Oczywiście skorzystaliśmy z założenia 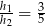 . Wiemy jeszcze, że
. Wiemy jeszcze, że 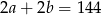 . Otrzymujemy stąd:
. Otrzymujemy stąd:
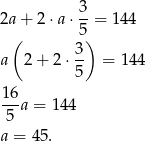
Ponadto 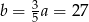 .
.
Odpowiedź: 27 i 45

