/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 7373461

Dodaj do ulubionych
Dodaj do rozwiązanych

Kąt ostry równoległoboku ma miarę 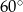∘ 6 0 . Stosunek kwadratów długości przekątnych jest równy 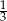13 . Wykaż, że ten równoległobok jest rombem.

Rozwiązanie

Oznaczmy długości boków równoległoboku przez a i b .

PIC

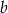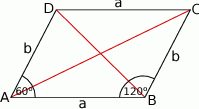
Piszemy teraz twierdzenia cosinusów w trójkątach 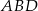ABD i ABC .

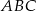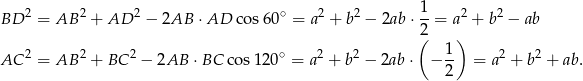
BD 2 = AB 2 + AD 2 − 2AB ⋅AD cos 60∘ = a2 + b2 − 2ab ⋅ 1-= a2 + b2 − ab 2( ) 2 2 2 ∘ 2 2 1- 2 2 AC = AB + BC − 2AB ⋅BC cos1 20 = a + b − 2ab ⋅ − 2 = a + b + ab.

Wykorzystujemy teraz podaną w treści zadania informację o stosunku kwadratów długości przekątnych.

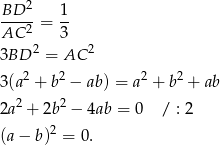
BD--2 1- AC 2 = 3 2 2 3BD = AC 3(a2 + b2 − ab) = a2 + b2 + ab 2 2 2a + 2b − 4ab = 0 / : 2 (a− b)2 = 0.

Zatem rzeczywiście 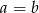a = b , czyli czworokąt 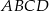ABCD jest rombem.

Wersja PDF