/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 7971733

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku 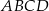ABCD przekątna 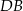DB ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26, 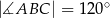|∡ABC | = 12 0∘ , oblicz długości boków równoległoboku.

Rozwiązanie

Zaczynamy od rysunku.

PIC

Sposób I

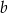Oznaczmy boki równoległoboku przez a i b . Mamy dwa równania (drugie to twierdzenie cosinusów w trójkącie ABD )

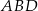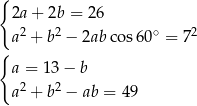
{ 2a + 2b = 2 6 2 2 ∘ 2 { a + b − 2abco s60 = 7 a = 13 − b a2 + b2 − ab = 49

Prowadzi to do równania

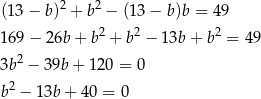
(13 − b)2 + b2 − (13 − b)b = 49 2 2 2 169 − 26b + b + b − 13b + b = 49 3b2 − 39b + 12 0 = 0 2 b − 13b + 40 = 0

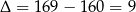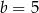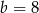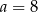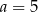Rozwiązujemy to równanie kwadratowe: Δ = 169 − 160 = 9 , b = 5 lub b = 8 . Mamy wtedy a = 8 lub a = 5 odpowiednio.

Sposób II

Tym razem dorysujmy wysokość 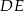DE . Z trójkąta 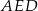AED mamy

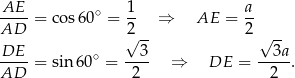
AE ∘ 1 a AD--= cos6 0 = 2- ⇒ AE = 2- √ -- √ -- DE--= sin60 ∘ = --3- ⇒ DE = --3a-. AD 2 2

Patrzymy teraz na trójkąt 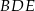BDE

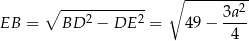
∘ --------- ∘ ----2------2 3a2- EB = BD − DE = 4 9− 4

Pozostało teraz skorzystać z podanego obwodu.

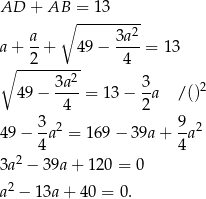
AD + AB = 13 ∘ --------2 a+ a-+ 49 − 3a--= 13 ∘ --2------ 4 3a 2 3 49 − ----= 13 − --a /()2 4 2 3-2 9- 2 49− 4a = 169− 39a + 4 a 3a2 − 39a+ 120 = 0 a2 − 1 3a+ 40 = 0.

No i mamy to samo równanie co w poprzednim sposobie.  
Odpowiedź: 5 i 8

Wersja PDF