Zadanie nr 9327053
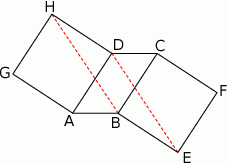
Na przeciwległych bokach równoległoboku 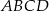 zbudowano kwadraty
zbudowano kwadraty 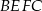 i
i 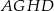 . Udowodnij, że proste
. Udowodnij, że proste 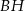 i
i 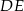 są równoległe.
są równoległe.
Rozwiązanie
Sposób I
Dorysujmy przekątną 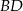 równoległoboku.
równoległoboku.
Zauważmy, że trójkąty 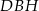 i
i 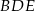 są przystające. Rzeczywiście, mają wspólny bok
są przystające. Rzeczywiście, mają wspólny bok 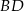 , ponadto
, ponadto 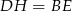 oraz
oraz
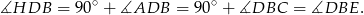
W szczególności,
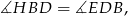
co oznacza, że proste 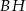 i
i 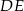 przecinają prostą
przecinają prostą 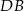 pod tym samym kątem.
pod tym samym kątem.
Sposób II
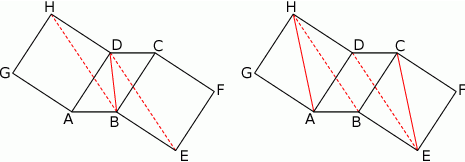
Tym razem dorysujmy przekątne 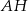 i
i 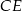 dorysowanych kwadratów. Zauważmy, że trójkąty
dorysowanych kwadratów. Zauważmy, że trójkąty 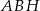 i
i 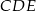 mają dwa boki równej długości (
mają dwa boki równej długości (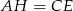 i
i 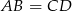 ) oraz
) oraz
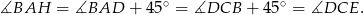
To oznacza, że trójkąty 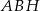 i
i 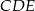 są przystające. W szczególności
są przystające. W szczególności 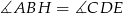 , co oznacza, że proste
, co oznacza, że proste 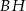 i
i 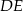 przecinają równoległe proste
przecinają równoległe proste 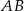 i
i 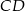 pod tym samym kątem. Proste
pod tym samym kątem. Proste 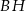 i
i 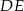 są więc równoległe.
są więc równoległe.
Sposób III
Zauważmy, że odcinki 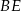 i
i 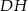 mają równe długości oraz są równoległe (bo są prostopadłe do równoległych odcinków
mają równe długości oraz są równoległe (bo są prostopadłe do równoległych odcinków 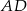 i
i 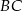 ). To oznacza, że w czworokącie
). To oznacza, że w czworokącie 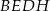 przeciwległe boki
przeciwległe boki 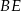 i
i 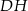 mają równą długość i są równoległe. Czworokąt ten jest więc równoległobokiem. Zatem jego pozostałe dwa boki
mają równą długość i są równoległe. Czworokąt ten jest więc równoległobokiem. Zatem jego pozostałe dwa boki 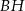 i
i 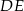 też są równoległe.
też są równoległe.

