Zadanie nr 2114917
Na rysunku przedstawiony jest przedział 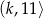 , gdzie
, gdzie 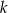 jest liczbą całkowitą. Suma wszystkich liczb całkowitych należących do tego przedziału jest równa
jest liczbą całkowitą. Suma wszystkich liczb całkowitych należących do tego przedziału jest równa 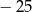 .
.
![]()
Stąd wynika, że
A) 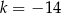 B)
B) 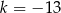 C)
C) 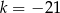 D)
D) 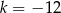
Rozwiązanie
Sposób I
Zauważmy, że suma liczb całkowitych w przedziale 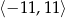 jest równa 0, więc suma liczb w przedziale
jest równa 0, więc suma liczb w przedziale 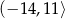 jest równa
jest równa 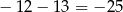 . Zatem
. Zatem 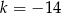 .
.
Sposób II
Liczby całkowite w danym przedziale są kolejnymi wyrazami ciągu arytmetycznego, w którym 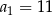 ,
, 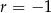 ,
, 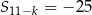 . Stąd
. Stąd
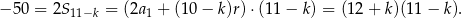
Teraz albo zgadujemy rozwiązanie dodatnie: 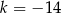 albo rozwiązujemy równanie kwadratowe
albo rozwiązujemy równanie kwadratowe
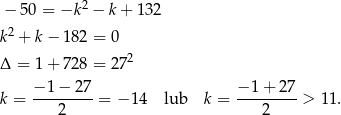
Odpowiedź: A

