/Szkoła średnia/Zadania testowe/Liczby/Liczby całkowite

Zadanie nr 3239420

Liczba 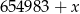6 54983 + x daje resztę 7 z dzielenia przez 9. Liczba x może być równa
A) 2 B) 3 C) 7 D) 8

Wersja PDF

Rozwiązanie

Sposób I

Z podanej informacji o reszcie wiemy, że liczba

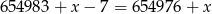
6 54983 + x − 7 = 654976 + x

jest liczbą podzielną przez 9. W takim razie suma cyfr tej liczby musi dzielić się przez 9. Suma cyfr liczby 654976 jest równa 37, więc x może być np. równe 8.

Sposób II

Dzielimy najpierw 654983 przez 9 z resztą. Ponieważ 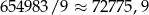654 983/9 ≈ 72775,9 mamy

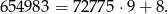
6 54983 = 7 2775 ⋅9+ 8.

Stąd

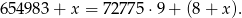
6 54983 + x = 72775 ⋅9+ (8+ x).

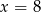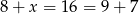Widać teraz, że reszta z dzielenia tej liczby przez 9 będzie równa 7 np. dla x = 8 (bo wtedy 8 + x = 16 = 9 + 7 ).  
Odpowiedź: D

Wersja PDF