/Szkoła średnia/Zadania testowe/Liczby/Liczby całkowite

Zadanie nr 6598624

Liczba dzielników naturalnych liczby 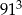3 91 jest równa
A) 8 B) 256 C) 16 D) 4

Wersja PDF

Rozwiązanie

Zauważmy najpierw, że 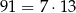91 = 7⋅13 . Stąd

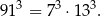
3 3 3 91 = 7 ⋅13 .

Sposób I

Wypisujemy dzielniki danej liczby

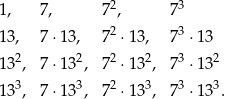
1 , 7, 72, 73 2 3 1 3, 7 ⋅13, 7 ⋅13 , 7 ⋅13 1 32, 7 ⋅132, 72 ⋅13 2, 73 ⋅132 1 33, 7 ⋅133, 72 ⋅13 3, 73 ⋅133.

Jest wiec 16 różnych dzielników

Sposób II

Dzielniki danej liczby są postaci

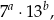
7a ⋅13b,

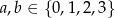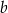gdzie a,b ∈ {0,1 ,2 ,3} . Ponieważ każdą z liczb a i b możemy wybrać na 4 sposoby, w sumie jest

4 ⋅4 = 16

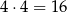
różnych dzielników.  
Odpowiedź: C

Wersja PDF