Zadanie nr 7321724
Na rysunku przedstawiony jest przedział 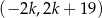 , gdzie
, gdzie 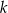 jest liczbą całkowitą. Suma wszystkich liczb całkowitych nieparzystych należących do tego przedziału jest równa 171.
jest liczbą całkowitą. Suma wszystkich liczb całkowitych nieparzystych należących do tego przedziału jest równa 171.
![]()
Stąd wynika, że
A) 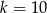 B)
B) 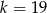 C)
C) 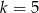 D)
D) 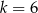
Rozwiązanie
Zauważmy, że suma liczb całkowitych nieparzystych w przedziale 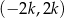 jest równa 0, więc suma liczb całkowitych nieparzystych w przedziale
jest równa 0, więc suma liczb całkowitych nieparzystych w przedziale 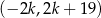 jest równa
jest równa
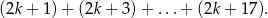
Jest to suma 9 kolejnych wyrazów ciągu arytmetycznego, więc mamy równanie
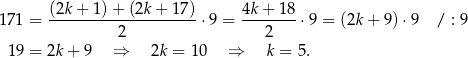
Odpowiedź: C

