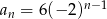Zadanie nr 6249224
Pierwszy wyraz ciągu geometrycznego 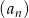 jest równy 6, a iloraz dziesiątego wyrazu i wyrazu szóstego równy jest 16. Wiedząc że ciąg
jest równy 6, a iloraz dziesiątego wyrazu i wyrazu szóstego równy jest 16. Wiedząc że ciąg 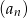 nie jest monotoniczny znajdź
nie jest monotoniczny znajdź
- jego iloraz,
- jego piąty wyraz,
- wzór na wyraz ogólny ciągu.
Rozwiązanie
- Korzystamy ze wzoru na wyraz ogólny ciągu gemoetrycznego
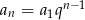 . W szczególności
. W szczególności 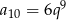 i
i 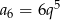 . Mamy zatem równanie
. Mamy zatem równanie 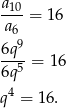
Zatem
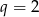 lub
lub 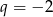 . Tylko
. Tylko 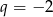 prowadzi do ciągu, który nie jest monotoniczny (dla
prowadzi do ciągu, który nie jest monotoniczny (dla 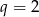 jest rosnący).
jest rosnący).
Odpowiedź: -2 - Korzystamy z poprzedniego podpunktu
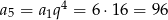 .
.
Odpowiedź: 96 - Z pierwszego podpunktu
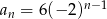 .
.
Odpowiedź: