/Szkoła średnia/Ciągi/Geometryczny/Dany przez iloczyny wyrazów

Zadanie nr 6591962

Iloczyn siedmiu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 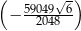( √-) − 59049-6 2048 . Oblicz czwarty wyraz tego ciągu.

Wersja PDF

Rozwiązanie

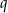Oznaczmy przez a pierwszy wyraz, a przez q iloraz tego ciągu. Ponieważ

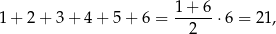
1 + 6 1+ 2+ 3+ 4+ 5+ 6 = ------⋅6 = 21 , 2

(suma początkowych wyrazów ciągu arytmetycznego), to mamy równanie

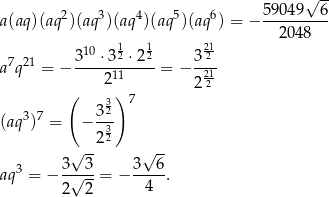
-- 59049√ 6 a(aq )(aq2)(aq3)(aq4)(aq5)(aq6) = − --------- 2048 7 21 310 ⋅312 ⋅212 3212 a q = − -----11----= − -21- ( 2) 2 2 332 7 (aq3)7 = − -3- 22 √ -- √ -- aq3 = − 3√-3-= − 3--6. 2 2 4

Otrzymane wyrażenie 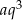aq3 to dokładnie czwarty wyraz tego ciągu.  
Odpowiedź: √ - 3--6 − 4

Wersja PDF