Zadanie nr 2228231
Dla jakich wartości  liczby
liczby 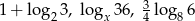 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Rozwiązanie
Ponieważ  jest w podstawie logarytmu, musi być
jest w podstawie logarytmu, musi być 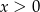 i
i 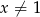 .
.
Liczby niezerowe 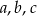 są trzema kolejnymi wyrazami ciągu geometrycznego jeżeli
są trzema kolejnymi wyrazami ciągu geometrycznego jeżeli 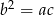 . Aby jakoś zapanować nad podstawami podanych logarytmów, zmienimy ich podstawy na 2.
. Aby jakoś zapanować nad podstawami podanych logarytmów, zmienimy ich podstawy na 2.
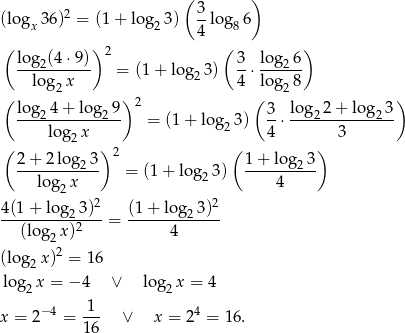
Odpowiedź: 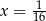 lub
lub