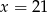/Szkoła średnia/Ciągi/Geometryczny/Trzywyrazowy

Zadanie nr 3519465

Dodaj do ulubionych
Dodaj do rozwiązanych

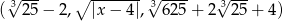Wyznacz x tak, aby ciąg √3--- ∘ -------√3---- 3√ --- ( 25 − 2, |x − 4|, 6 25+ 2 25 + 4) był ciągiem geometrycznym.

Rozwiązanie

Musimy sprawdzić kiedy kwadrat środkowego wyrazu jest iloczynem wyrazów sąsiednich.

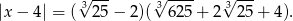
3√ --- 3√ ---- √3--- |x− 4| = ( 25− 2)( 625 + 2 2 5+ 4 ).

Można prawą stronę wymnożyć, ale można też zauważyć, że jest wzór

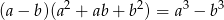
(a − b)(a 2 + ab + b2) = a3 − b 3

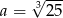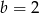napisany dla √ --- a = 3 25 i b = 2 . Mamy więc

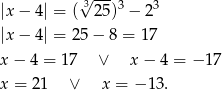
√ --- |x− 4| = ( 3 25)3 − 23 |x− 4| = 25− 8 = 17 x− 4 = 17 ∨ x− 4 = − 17 x = 21 ∨ x = − 13.

 
Odpowiedź: 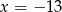x = − 13 lub x = 21

Wersja PDF