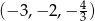/Szkoła średnia/Ciągi/Geometryczny/Trzywyrazowy

Zadanie nr 9636465

Dodaj do ulubionych
Dodaj do rozwiązanych

Trzywyrazowy ciąg geometryczny jest rosnący. Iloczyn wszystkich wyrazów tego ciągu jest równy -8, a iloraz pierwszego wyrazu przez trzeci wynosi 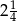214 . Wyznacz ten ciąg.

Rozwiązanie

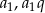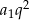Jeżeli oznaczymy wyrazy podanego ciągu przez a 1,a 1q i 2 a1q , to z drugiego z podanych warunków mamy

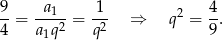
9-= -a1--= -1- ⇒ q2 = 4-. 4 a1q2 q 2 9

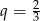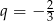Zatem q = 23 lub q = − 23 . Drugie z tych rozwiązań odrzucamy bo ciąg ma być rosnący. Z pierwszego warunku mamy

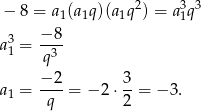
− 8 = a1(a1q)(a 1q 2) = a31q3 −8 a31 = ---- q3 −2 3 a1 = -q-= − 2 ⋅2-= − 3 .

 
Odpowiedź: 4 (− 3,− 2,− 3)

Wersja PDF