/Szkoła średnia/Geometria/Geometria analityczna/Okrąg

Zadanie nr 1496043

Dodaj do ulubionych
Dodaj do rozwiązanych

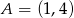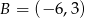Środek okręgu przechodzącego przez punkty A = (1,4) i B = (− 6,3 ) leży na osi 0x .

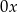  • Wyznacz równanie tego okręgu.
  • Wyznacz równanie prostej prostopadłej do prostej 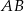AB i oddalonej od początku układu współrzędnych o √ -- 2 .

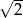Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

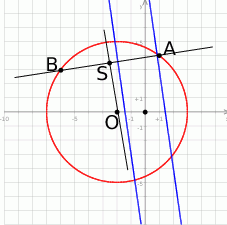
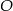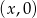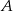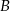  • Środek O okręgu możemy wyznaczyć szukając punktu (x ,0) , który jest równo odległy od punktów A i B , ale ponieważ i tak będziemy musieli pisać proste prostopadłe do 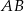AB (w następnym podpunkcie), to zrobimy to inaczej: napiszemy równanie symetralnej odcinka 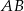AB i znajdziemy jej punkt wspólny z osią Ox .

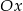    Symetralna musi przechodzić przez środek odcinka 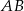AB , czyli przez punkt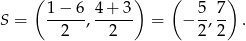

    ( ) ( ) 1-−-6- 4+--3- 5-7- S = 2 , 2 = − 2,2 .

    Równanie symetralnej możemy napisać pisząc najpierw równanie prostej 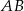AB i potem szukając prostej prostopadłej do niej i przechodzącej przez 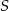S . Znacznie prościej jest jednak skorzystać ze wzoru na równanie prostej prostopadłej do wektora →v = [p,q] i przechodzącej przez punkt (x0,y0)

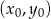
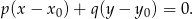
    p (x− x0)+ q(y− y0) = 0.

    W naszej sytuacji mamy → → v = AB = [− 7,− 1] . Daje to nam prostą

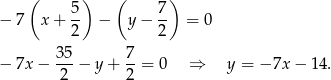
    ( 5) ( 7) − 7 x+ -- − y− -- = 0 2 2 35- 7- − 7x − 2 − y + 2 = 0 ⇒ y = −7x − 14.

    Prosta ta przecina oś 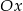Ox w punkcie 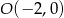O (− 2,0) . Wyliczmy jeszcze promień okręgu.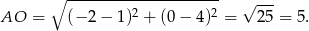

    ∘ --------------------- --- AO = (−2 − 1 )2 + (0 − 4)2 = √ 2 5 = 5.

    Zatem szukane równanie okręgu to

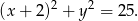
    2 2 (x + 2) + y = 25 .

     
    Odpowiedź: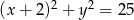 (x + 2)2 + y2 = 25

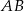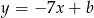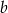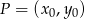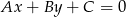  • Wiemy już, że proste prostopadłe do AB są postaci y = − 7x+ b . Współczynnik b wyznaczymy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :
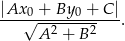
    |Ax-0 +-By0-+-C-| √ --2----2- . A + B

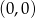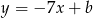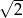    W naszej sytuacji punkt (0,0) ma być odległy od prostej y = − 7x + b o √ -- 2 , co daje nam równanie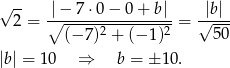

    √ -- |− 7 ⋅0 − 0 + b| |b| 2 = ∘-----------------= √---- (−7 )2 + (− 1)2 50 |b| = 1 0 ⇒ b = ± 10.

     
    Odpowiedź: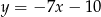 y = −7x − 10 i y = − 7x + 10

Wersja PDF