Zadanie nr 5216866
Dane są dwa okręgi o równaniach 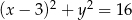 i
i 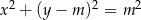 ,
, 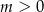 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 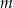 , dla których te okręgi mają jeden punkt wspólny.
, dla których te okręgi mają jeden punkt wspólny.
Rozwiązanie
Sposób I
Jeżeli okręgi mają mieć jeden punkt wspólny, to muszą być styczne, czyli odległość ich środków musi być równa sumie lub różnicy ich promieni (w zależności od tego, czy styczność ma być zewnętrzna, czy wewnętrzna). Pierwszy okrąg ma środek 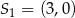 i promień
i promień 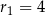 , a drugi ma środek
, a drugi ma środek 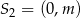 i promień
i promień 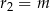 . Mamy zatem 3 możliwości
. Mamy zatem 3 możliwości
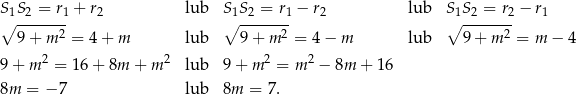
Ponieważ z założenia 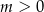 , mamy stąd
, mamy stąd 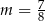 .
.
Sposób II
Musimy ustalić kiedy układ równań
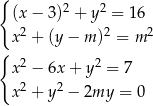
ma dokładnie jedno rozwiązanie. Odejmujemy od drugiego równania pierwsze i mamy
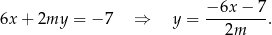
Podstawiamy tę wartość 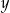 do pierwszego równania i mamy
do pierwszego równania i mamy
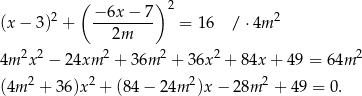
Powyższe równanie ma mieć dokładnie jedno rozwiązanie, więc musi być spełniony warunek
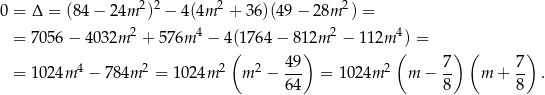
Ponieważ interesują nas tylko dodatnie wartości 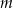 , mamy stąd
, mamy stąd 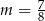 .
.
Na koniec obrazek.
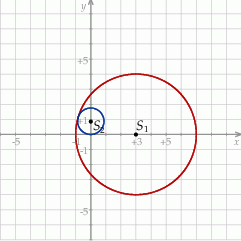
Odpowiedź: