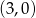Zadanie nr 5244840
Wyznacz współrzędne punktów wspólnych prostej 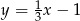 i okręgu
i okręgu 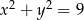 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
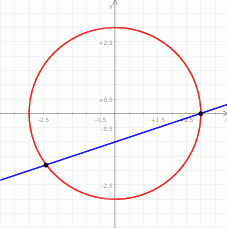
Wstawiamy 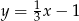 do równania okręgu.
do równania okręgu.
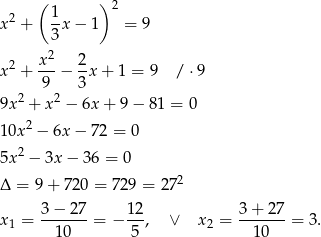
Mamy wtedy odpowiednio
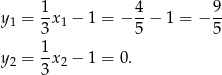
Odpowiedź: 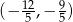 i
i 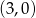
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz współrzędne punktów wspólnych prostej 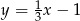 i okręgu
i okręgu 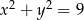 .
.
Zaczynamy od szkicowego rysunku.

Wstawiamy 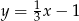 do równania okręgu.
do równania okręgu.
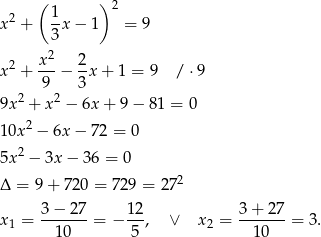
Mamy wtedy odpowiednio
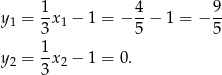
Odpowiedź: 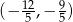 i
i