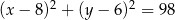Zadanie nr 6554210
Środki okręgów 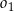 i
i 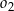 znajdują się po różnych stronach prostej
znajdują się po różnych stronach prostej 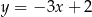 , która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu
, która zawiera punkty wspólne tych okręgów. Wiedząc, że promień okręgu 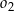 jest równy
jest równy 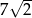 oraz, że okrąg
oraz, że okrąg 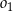 ma równanie
ma równanie 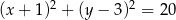 , wyznacz równanie okręgu
, wyznacz równanie okręgu 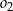 .
.
Rozwiązanie
Rozpoczynamy oczywiście od szkicowego rysunku.
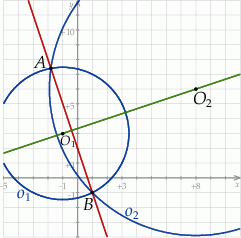
Na początku wyznaczmy punkty wspólne podanych: okręgu i prostej. Podstawiamy 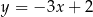 do równania okręgu.
do równania okręgu.
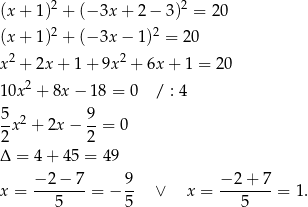
Stąd 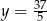 i
i 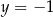 odpowiednio. Zatem punkty przecięcia to
odpowiednio. Zatem punkty przecięcia to 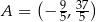 oraz
oraz 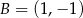 .
.
Kolejna rzecz, którą możemy zrobić, to napisać równanie prostej 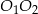 przechodzącej przez środki obu okręgów. Prosta ta musi być prostopadła do danej prostej
przechodzącej przez środki obu okręgów. Prosta ta musi być prostopadła do danej prostej 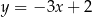 oraz musi przechodzić przez punkt
oraz musi przechodzić przez punkt 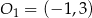 . Szukamy zatem prostej postaci
. Szukamy zatem prostej postaci 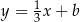 – współczynnik
– współczynnik 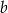 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 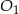 .
.
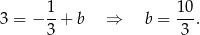
Zatem prosta 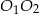 ma równanie
ma równanie 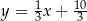 i pozostało znaleźć na niej punkt
i pozostało znaleźć na niej punkt 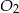 , który jest odległy od punktu
, który jest odległy od punktu 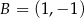 o
o 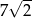 . Powiedzmy, że szukany punkt to
. Powiedzmy, że szukany punkt to 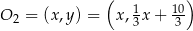 . Mamy zatem
. Mamy zatem
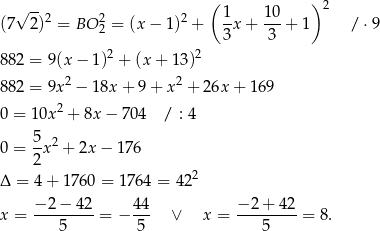
Pierwszy pierwiastek daje punkt, który leży po tej samej stronie prostej 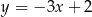 co punkt
co punkt 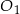 , a to jest sprzeczne z założeniem. Zatem
, a to jest sprzeczne z założeniem. Zatem 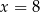 ,
,
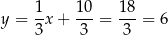
oraz 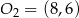 . Możemy teraz napisać szukane równanie okręgu
. Możemy teraz napisać szukane równanie okręgu 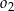 .
.
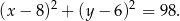
Odpowiedź: