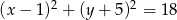Zadanie nr 8629618
Napisz równanie okręgu, który jest styczny do prostej 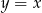 w punkcie
w punkcie 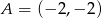 , oraz który odcina z prostej
, oraz który odcina z prostej 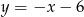 cięciwę o długości 8.
cięciwę o długości 8.
Rozwiązanie
Dane proste są do siebie prostopadłe. Sprawdźmy jeszcze jaki jest ich punkt przecięcia.
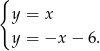
Podstawiamy z pierwszego równania do drugiego.
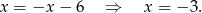
Stąd 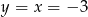 i punkt wspólny prostych to
i punkt wspólny prostych to 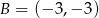 . Teraz możemy wykonać szkicowy rysunek.
. Teraz możemy wykonać szkicowy rysunek.
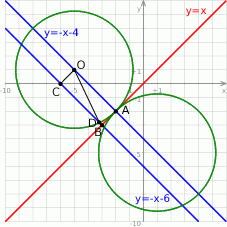
Ponieważ okrąg ma być styczny do prostej 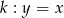 w punkcie
w punkcie 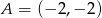 , jego środek
, jego środek 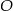 musi leżeć na prostej prostopadłej do
musi leżeć na prostej prostopadłej do 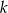 i przechodzącej przez punkt
i przechodzącej przez punkt 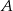 . Wyznaczmy równanie tej prostej. Ma ona postać
. Wyznaczmy równanie tej prostej. Ma ona postać 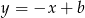 liczbę
liczbę 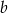 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 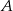 .
.
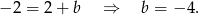
Zatem środek 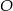 okręgu leży na prostej
okręgu leży na prostej 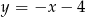 .
.
Zrobiliśmy rzeczy, które były oczywiste, więc pora teraz na chwilę zastanowienia. Niech 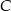 będzie środkiem cięciwy wyciętej przez okrąg z danej prostej
będzie środkiem cięciwy wyciętej przez okrąg z danej prostej 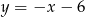 . Zauważmy, że trójkąt
. Zauważmy, że trójkąt 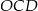 jest prostokątny i możemy łatwo obliczyć długości jego przyprostokątnych:
jest prostokątny i możemy łatwo obliczyć długości jego przyprostokątnych: 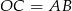 , a
, a 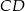 to połowa długości cięciwy. Możemy więc łatwo obliczyć długość promienia okręgu
to połowa długości cięciwy. Możemy więc łatwo obliczyć długość promienia okręgu 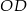 . Liczymy
. Liczymy
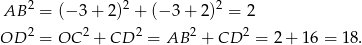
Promień okręgu jest więc równy 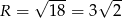 . Szukamy teraz punktu
. Szukamy teraz punktu 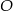 na prostej
na prostej 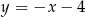 , który jest odległy od
, który jest odległy od 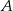 o
o 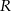 . Szukamy punktu
. Szukamy punktu 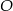 postaci
postaci 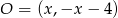 .
.
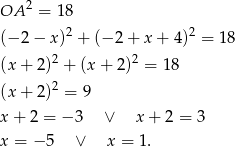
Stąd 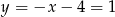 i
i 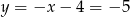 odpowiednio. Są zatem dwa okręgi spełniające warunki zadania
odpowiednio. Są zatem dwa okręgi spełniające warunki zadania
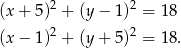
Odpowiedź: 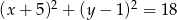 i
i