/Szkoła średnia/Geometria/Geometria analityczna/Okrąg

Zadanie nr 8884692

Dodaj do ulubionych
Dodaj do rozwiązanych

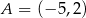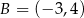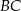W układzie współrzędnych punkty A = (− 5 ,2 ) i B = (− 3,4) są końcami cięciwy okręgu o . Średnica BC tego okręgu jest zwarta w prostej o równaniu 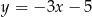y = − 3x− 5 . Wyznacz współrzędne punktu C .

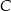Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

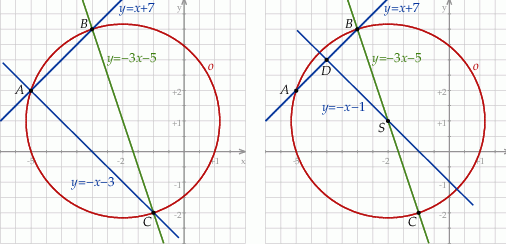
Sposób I

Napiszmy najpierw równanie prostej 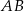AB . Szukamy prostej w postaci 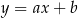y = ax + b i podstawiamy współrzędne punktów 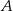A i B .

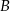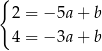
{ 2 = − 5a+ b 4 = − 3a+ b

Odejmujemy od drugiego równania pierwsze i mamy

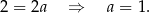
2 = 2a ⇒ a = 1.

Stąd 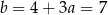b = 4 + 3a = 7 i prosta 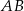AB ma równanie y = x + 7 .

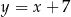Ponieważ 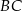BC jest średnicą okręgu, to 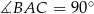∘ ∡BAC = 90 . To pozwala łatwo wyznaczyć punkt 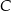C – jest to punkt wspólny podanej prostej 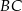BC i prostej prostopadłej do 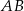AB przechodzącej przez 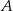A . Prosta prostopadła do 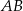AB ma równanie postaci 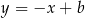y = −x + b . Współczynnik 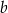b wyznaczamy podstawiając współrzędne punktu A .

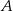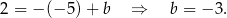
2 = − (−5 )+ b ⇒ b = − 3.

Zatem prosta 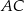AC ma równanie 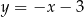y = −x − 3 i pozostało znaleźć jej punkt wspólny z prostą BC .

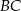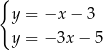
{ y = −x − 3 y = − 3x− 5

Odejmujemy od pierwszego równania drugie i mamy

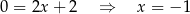
0 = 2x + 2 ⇒ x = − 1

Stąd 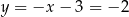y = −x − 3 = −2 i C = (− 1,− 2) .

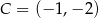Sposób II

Tym razem najpierw wyznaczymy środek 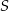S danego okręgu – jest to punkt wspólny symetralnej odcinka 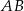AB i danej średnicy 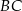BC . Symetralna odcinka 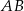AB to zbiór punktów 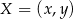X = (x ,y ) spełniających warunek

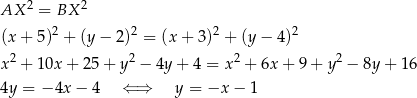
2 2 AX = BX (x + 5)2 + (y − 2)2 = (x + 3 )2 + (y − 4)2 x 2 + 10x + 25+ y2 − 4y+ 4 = x2 + 6x + 9 + y2 − 8y + 1 6 4y = − 4x − 4 ⇐ ⇒ y = −x − 1

Szukamy teraz punktu wspólnego 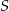S tej symetralnej z daną średnicą BC .

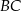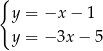
{ y = −x − 1 y = − 3x− 5

Odejmujemy od pierwszego równania drugie i mamy

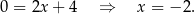
0 = 2x + 4 ⇒ x = − 2.

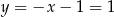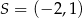Stąd y = −x − 1 = 1 i S = (− 2,1) . Korzystamy teraz z tego, że 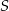S jest środkiem średnicy BC .

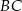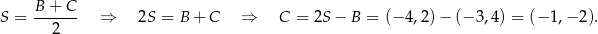
B + C S = ------ ⇒ 2S = B + C ⇒ C = 2S − B = (− 4,2)− (− 3,4 ) = (− 1,− 2). 2

 
Odpowiedź: C = (− 1,− 2)

Wersja PDF