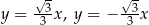Zadanie nr 9338176
Wyznacz równanie prostych przechodzących przez początek układu współrzędnych i stycznych do okręgu o środku w punkcie 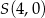 i promieniu
i promieniu 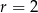 .
.
Rozwiązanie
Zaczynamy od rysunku.
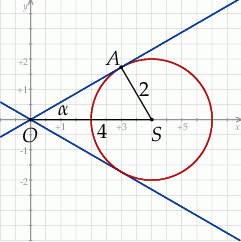
Proste przchodzące przez początek układu są postaci 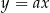 (tak naprawdę jedna z nich nie jest tej postaci:
(tak naprawdę jedna z nich nie jest tej postaci: 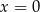 , ale widać, że nie jest to szukana styczna). Musimy zatem wyznaczyć współczynnik
, ale widać, że nie jest to szukana styczna). Musimy zatem wyznaczyć współczynnik  (z rysunku widać, że będą to dwie wartości wzajemnie przeciwne).
(z rysunku widać, że będą to dwie wartości wzajemnie przeciwne).
Sposób I
Współczynnik kierunkowy  prostej
prostej 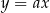 to dokładnie tangens kąta jaki ta prosta tworzy z osią
to dokładnie tangens kąta jaki ta prosta tworzy z osią 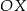 . Z twierdzenia Pitagorasa w trójkącie
. Z twierdzenia Pitagorasa w trójkącie 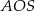 mamy
mamy
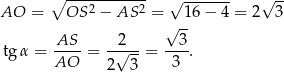
Druga wartość  to
to 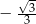 .
.
Sposób II
Tym razem wstawmy równanie prostej 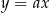 do równania okręgu i sprawdźmy kiedy mają dokładnie jeden punkt wspólny.
do równania okręgu i sprawdźmy kiedy mają dokładnie jeden punkt wspólny.
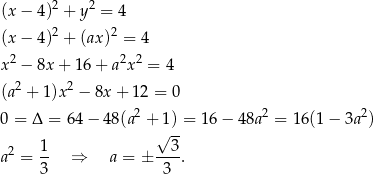
Sposób III
Tym razem skorzystamy ze wzoru na odległość punktu 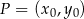 od prostej
od prostej 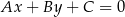 :
:
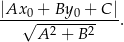
Prosta jest styczna do okręgu dokładnie wtedy, gdy odległość od niej środka tego okręgu jest równa jego promieniowi. Pytanie zatem brzmi: kiedy punkt 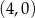 jest odległy od prostej
jest odległy od prostej 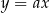 o 2? Daje to nam równanie
o 2? Daje to nam równanie
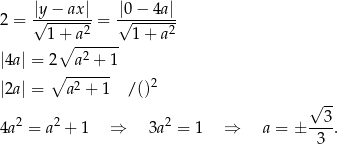
Sposób IV
Na mocy twierdzenia Pitagorasa
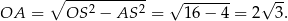
Zatem pole trójkąta 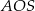 jest równe
jest równe
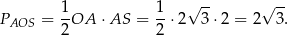
To z kolei pozwala wyliczyć długość 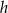 wysokości trójkąta
wysokości trójkąta 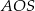 opuszczonej z wierzchołka
opuszczonej z wierzchołka 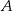 .
.
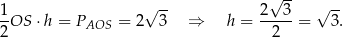
To oznacza, że druga współrzędna punktu 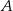 jest równa
jest równa 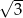 lub
lub 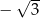 (dla punktu poniżej osi
(dla punktu poniżej osi 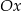 ). Pierwszą współrzędną możemy wyliczyć z równania okręgu.
). Pierwszą współrzędną możemy wyliczyć z równania okręgu.
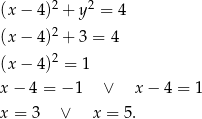
Z rysunku widać, że musi być 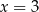 , czyli
, czyli 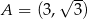 lub
lub 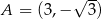 . Teraz pozostało sprawdzić dla jakiej wartości
. Teraz pozostało sprawdzić dla jakiej wartości  prosta
prosta 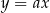 przechodzi przez punkt
przechodzi przez punkt 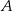 . Mamy odpowiednio (podstawiamy współrzędne punktu do równania prostej)
. Mamy odpowiednio (podstawiamy współrzędne punktu do równania prostej)
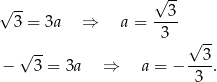
Zatem szukane proste to 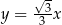 i
i 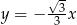 .
.
Odpowiedź: