Zadanie nr 2036300

Wykres funkcji liniowej 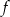przechodzi przez punkt 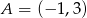A = (− 1,3) i ma dokładnie jeden punkt wspólny z parabolą o równaniu 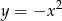y = −x 2 . Znajdź wzór funkcji .

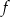Rozwiązanie

Szukamy funkcji postaci 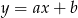y = ax + b . To, że wykres przechodzi przez punkt 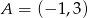A = (− 1,3) daje nam

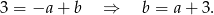
3 = −a + b ⇒ b = a + 3.

Prosta 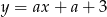y = ax + a + 3 będzie przecinać podaną parabolę w dokładnie jednym punkcie jeżeli układ równań

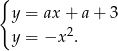
{ y = ax + a + 3 2 y = −x .

ma dokładnie jedno rozwiązanie. Odejmując równania stronami (żeby skrócić 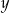) mamy

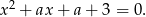
x2 + ax + a + 3 = 0.

Równanie to będzie miało dokładnie jedno rozwiązanie gdy 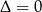Δ = 0 .

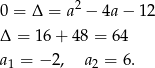
2 0 = Δ = a − 4a − 12 Δ = 16 + 48 = 64 a1 = −2 , a2 = 6.

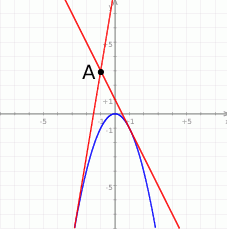
Na koniec, dla ciekawskich, wykres opisanej sytuacji.

Odpowiedź: 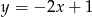y = −2x + 1 lub y = 6x + 9

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz