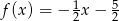/Szkoła średnia/Funkcje - wykresy/Liniowy/Wzór z wykresu

Zadanie nr 8881197

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykres funkcji liniowej 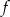f przechodzi przez punkt 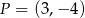P = (3,− 4) , a zbiorem rozwiązań nierówności 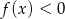f (x) < 0 jest przedział 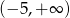(− 5,+ ∞ ) . Wyznacz wzór funkcji f .

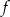Rozwiązanie

Z podanych informacji wynika, że wykresem funkcji 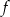f jest prosta, która przechodzi przez punkt 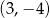(3,− 4) oraz znajduje się poniżej osi 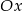Ox dokładnie na przedziale 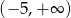(− 5,+ ∞ ) . To oznacza, że prosta ta musi przecinać oś 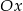Ox w punkcie 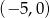(− 5,0) . Wystarczy zatem napisać równanie prostej przechodzącej przez punkty 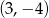(3 ,− 4 ) i (− 5 ,0 ) .

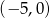Szukamy prostej w postaci 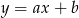y = ax + b . Podstawiamy współrzędne punktów i mamy układ równań.

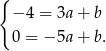
{ − 4 = 3a+ b 0 = − 5a+ b.

Odejmujemy od pierwszego równania drugie i otrzymujemy

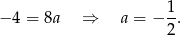
1 − 4 = 8a ⇒ a = − -. 2

Z drugiego równania mamy

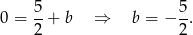
5 5 0 = 2-+ b ⇒ b = − 2-.

Stąd 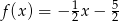f(x) = − 1x − 5 2 2 .  
Odpowiedź: 1 5 f(x ) = − 2x − 2

Wersja PDF