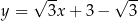/Szkoła średnia/Funkcje - wykresy/Liniowy/Wzór z wykresu

Zadanie nr 9535254

Wyznacz wzór funkcji liniowej, wiedząc że jej wykres jest nachylony do osi 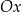Ox pod kątem 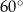60∘ i przechodzi przez punkt P = (1 ,3 ) .

Wersja PDF

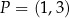Rozwiązanie

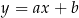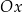Szukamy funkcji postaci y = ax + b . Wiadomo, że współczynnik kierunkowy a jest równy tangensowi kąta pod jakim wykres tej funkcji jest nachylony do osi Ox . W naszym przypadku mamy więc

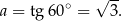
√ -- a = tg60∘ = 3.

Współczynnik 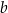b wyznaczymy dzięki informacji o tym, że wykres przechodzi przez punkt (1,3) .

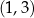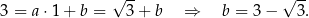
√ -- √ -- 3 = a ⋅1+ b = 3 + b ⇒ b = 3− 3.

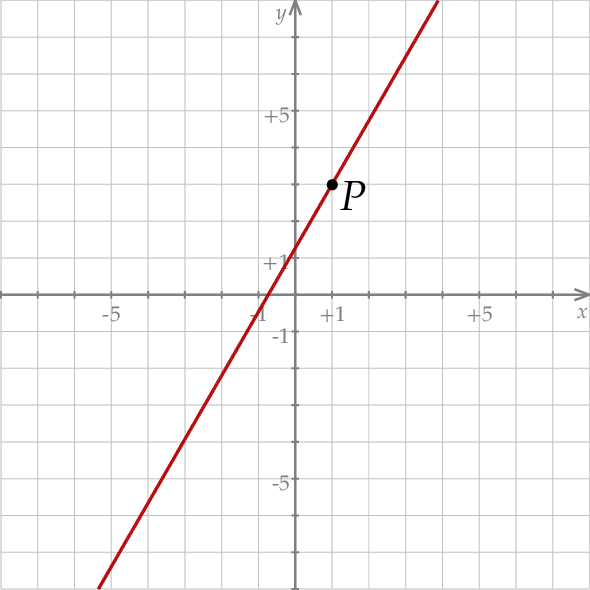
Na koniec, dla ciekawskich, wykres funkcji.

PIC

 
Odpowiedź: √ -- √ -- y = 3x + 3 − 3

Wersja PDF