Zadanie nr 1238943
Znajdź równanie okręgu stycznego do prostej 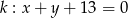 i do prostej
i do prostej 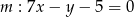 w punkcie
w punkcie 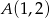 .
.
Rozwiązanie
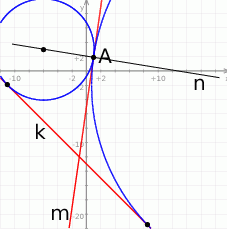
Oczywiście najważniejszy jest szkic opisanej sytuacji – widać, że będą dwa takie okręgi.
Informacja o tym, że okrąg jest styczny do prostej 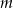 w punkcie
w punkcie 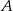 oznacza, że jego środek
oznacza, że jego środek 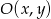 leży na prostej
leży na prostej  prostopadłej do
prostopadłej do 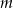 i przechodzącej przez punkt
i przechodzącej przez punkt 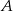 . Prosta ta jest postaci
. Prosta ta jest postaci 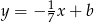 . Współczynnik
. Współczynnik 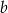 wyznaczamy wstawiając współrzędne punktu
wyznaczamy wstawiając współrzędne punktu 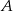 .
.
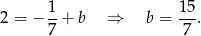
Aby nie mieć ułamków możemy tę prostą zapisać w postaci 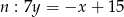 . Środek szukanego okręgu jest więc postaci
. Środek szukanego okręgu jest więc postaci 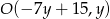 .
.
Pozostało wyznaczyć taką wartość 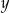 , dla której odległości punktu
, dla której odległości punktu 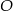 od prostych
od prostych 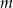 i
i 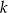 są równe. Można to zrobić na kilka sposobów, my pokażemy dwa z nich.
są równe. Można to zrobić na kilka sposobów, my pokażemy dwa z nich.
Sposób I
Skorzystamy ze wzoru na odległość punktu 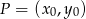 od prostej
od prostej 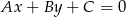 :
:
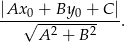
W naszej sytuacji mamy równanie
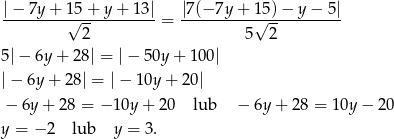
Otrzymaliśmy więc dwa punkty 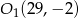 i
i 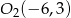 . Dla każdego z tych punktów wyliczmy jego odległość od puntu
. Dla każdego z tych punktów wyliczmy jego odległość od puntu 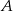 (czyli promień szukanego okręgu).
(czyli promień szukanego okręgu).
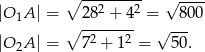
Daje to nam równania okręgów 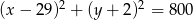 lub
lub 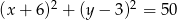 .
.
Sposób II
Tym razem napiszemy równanie okręgu o środku 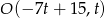 i przechodzącego przez
i przechodzącego przez 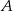 . Następnie sprawdzimy kiedy (dla jakiego
. Następnie sprawdzimy kiedy (dla jakiego 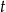 ) jest on styczny do prostej
) jest on styczny do prostej 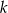 . Policzmy promień tego okręgu
. Policzmy promień tego okręgu
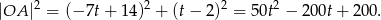
Musimy więc ustalić, kiedy okrąg
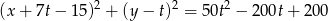
ma dokładnie jeden punkt wspólny z prostą 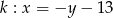 . Podstawiamy do równania
. Podstawiamy do równania
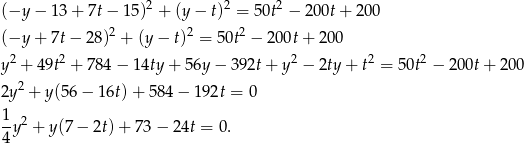
Równanie to ma jedno rozwiązanie gdy 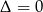 , czyli
, czyli
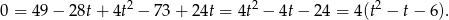
Dalej 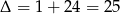 ,
, 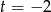 lub
lub 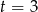 . Stąd otrzymujemy dwa równania okręgów
. Stąd otrzymujemy dwa równania okręgów 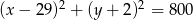 lub
lub 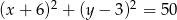 .
.
Odpowiedź: 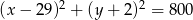 lub
lub