/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczny do prostej

Zadanie nr 2270894

Dodaj do ulubionych
Dodaj do rozwiązanych

Napisz równanie okręgu stycznego do osi 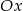Ox układu współrzędnych o promieniu równym 5 oraz środku należącym do prostej 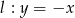l : y = −x i do drugiej ćwiartki układu współrzędnych. Napisz równanie stycznej do tego okręgu prostopadłej do l .

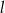Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

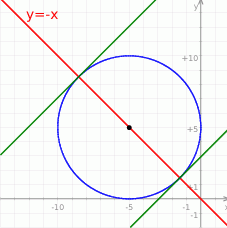
Skoro okrąg ma być styczny od osi 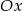Ox , to jego odległość od tej osi musi być równa promieniowi. Wiemy ponadto, że leży on w II ćwiartce, zatem druga współrzędna środka musi być równa 5. Dodatkowo wiemy, że środek leży na prostej 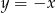y = −x , więc pierwsza współrzędna środka równa się -5 i okrąg ma równanie

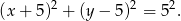
2 2 2 (x+ 5) + (y − 5 ) = 5 .

Pozostało napisać równania stycznych. Mają one być prostopadłe do prostej 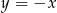y = −x , więc mają postać 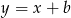y = x + b . Współczynnik 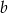b wyznaczymy na dwa sposoby.

Sposób I

Odległość środka okręgu od każdej stycznej jest równa promieniowi, czyli w naszej sytuacji jest równa 5. Ze wzoru na odległość punktu od prostej otrzymujemy w ten sposób równanie

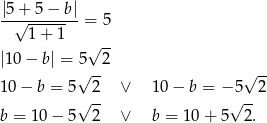
|5+ 5− b| --√--------= 5 1+ 1 √ -- |1 0− b| = 5 2 √ -- √ -- 10− b = 5 2 ∨ 10− b = − 5 2 b = 10 − 5√ 2- ∨ b = 10 + 5√ 2.

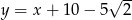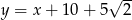Zatem szukane styczne to √ -- y = x + 10 − 5 2 oraz √ -- y = x+ 10+ 5 2 .

Sposób II

Sprawdźmy kiedy prosta 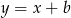y = x + b i dany okrąg mają dokładnie jeden punkt wspólny (podstawiamy do równania okręgu).

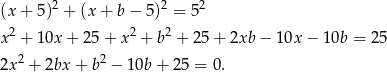
(x + 5)2 + (x + b − 5 )2 = 52 2 2 2 x + 10x + 25 + x + b + 25 + 2xb − 10x − 10b = 25 2x2 + 2bx + b2 − 10b + 25 = 0.

Równanie kwadratowe ma dokładnie jedno rozwiązanie jeżeli 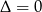Δ = 0 , czyli

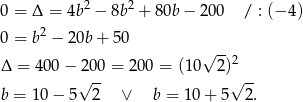
2 2 0 = Δ = 4b − 8b + 8 0b− 200 / : (− 4) 0 = b2 − 2 0b+ 50 √ -- Δ = 400 − 20 0 = 200 = (1 0 2)2 √ -- √ -- b = 10− 5 2 ∨ b = 1 0+ 5 2.

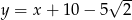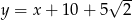Zatem szukane styczne to √ -- y = x + 10 − 5 2 oraz √ -- y = x+ 10+ 5 2 .  
Odpowiedź: 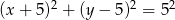(x + 5)2 + (y − 5)2 = 52 , styczne: √ -- √ -- y = x+ 10− 5 2, y = x + 10 + 5 2

Wersja PDF