Zadanie nr 2365104
Okrąg o środku 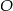 jest wpisany w trójkąt
jest wpisany w trójkąt 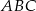 , gdzie
, gdzie 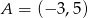 . Wiedząc, że okrąg ten jest styczny do boków
. Wiedząc, że okrąg ten jest styczny do boków 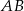 i
i 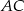 odpowiednio w punktach
odpowiednio w punktach 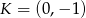 i
i 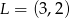 oblicz długość odcinka
oblicz długość odcinka 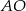 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
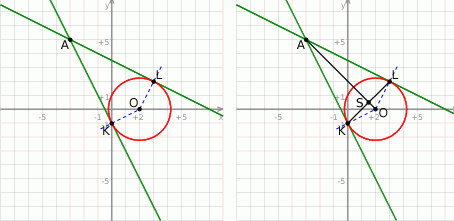
Plan jest następujący: skoro interesujący nas okrąg jest styczny do prostych 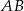 i
i 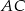 w punktach
w punktach 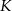 i
i 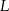 to punkt
to punkt  leży na przecięciu prostych przechodzących przez te punkty i prostopadłych odpowiednio do boków
leży na przecięciu prostych przechodzących przez te punkty i prostopadłych odpowiednio do boków 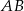 i
i 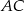 . Napiszemy więc równania prostych
. Napiszemy więc równania prostych 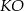 i
i 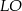 , a to pozwoli wyliczyć współrzędne punktu
, a to pozwoli wyliczyć współrzędne punktu 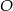 .
.
Sposób I
Aby napisać równania prostych 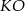 i
i 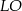 skorzystamy z równania
skorzystamy z równania
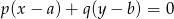
prostej prostopadłej do wektora ![→ v = [p ,q]](https://img.zadania.info/zad/2365104/HzadR14x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 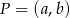 .
.
W przypadku prostej 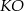 mamy
mamy
![−→ →v = AK = [0 − (− 3),− 1 − 5] = [3,− 6]](https://img.zadania.info/zad/2365104/HzadR17x.gif)
oraz 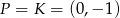 . Zatem prosta
. Zatem prosta 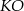 ma równanie
ma równanie
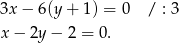
W przypadku prostej 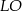 mamy
mamy
![→v = −A→L = [3 − (− 3),2 − 5] = [6,− 3]](https://img.zadania.info/zad/2365104/HzadR22x.gif)
oraz 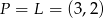 . Zatem prosta
. Zatem prosta 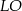 ma równanie
ma równanie
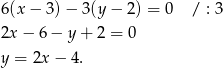
Szukamy teraz punktu wspólnego tych dwóch prostych.
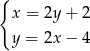
Podstawiając 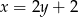 z pierwszego równania do drugiego mamy
z pierwszego równania do drugiego mamy
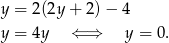
Zatem 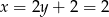 i
i 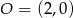 .
.
Teraz bez trudu liczymy żądaną odległość
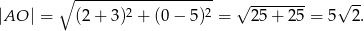
Sposób II
Jeżeli nie chcemy korzystać ze wzoru na równanie prostej prostopadłej do wektora to możemy równania prostych 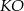 i
i 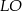 wyznaczyć bardziej konwencjonalnie – wyznaczając najpierw równania prostych
wyznaczyć bardziej konwencjonalnie – wyznaczając najpierw równania prostych 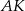 i
i 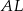 , potem pisząc równania prostych do nich prostopadłych i przechodzących odpowiednio przez punkty
, potem pisząc równania prostych do nich prostopadłych i przechodzących odpowiednio przez punkty 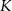 i
i 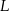 .
.
Możemy oczywiście korzystać z równania prostej przechodzącej przez dwa punkty, ale my będziemy unikać tego wzoru, bo raczej nie upraszcza on rachunków.
Szukamy prostej w postaci 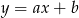 przechodzącej przez
przechodzącej przez 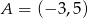 i
i 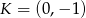 .
.
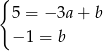
Odejmując od pierwszego równania drugie mamy 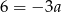 , czyli
, czyli 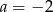 i prosta
i prosta 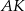 ma równanie
ma równanie 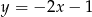 .
.
Od razu wyznaczmy równanie prostej 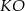 . Jest ona prostopadła do
. Jest ona prostopadła do 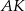 , więc ma postać
, więc ma postać 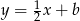 . Współczynnik
. Współczynnik 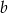 wyznaczmy podstawiając współrzędne punktu
wyznaczmy podstawiając współrzędne punktu 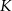 ,
, 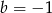 . Zatem prosta ta ma równanie
. Zatem prosta ta ma równanie 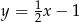
Teraz szukamy prostej 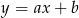 przechodzącej przez
przechodzącej przez 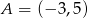 i
i 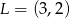 .
.
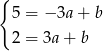
Odejmując od pierwszego równania drugie mamy 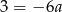 , czyli
, czyli 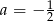 . Współczynnik
. Współczynnik 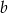 nie jest nam potrzebny, więc możemy go nie liczyć.
nie jest nam potrzebny, więc możemy go nie liczyć.
Wyznaczmy teraz równanie prostej 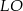 . Jest ona prostopadła do
. Jest ona prostopadła do 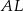 , więc ma postać
, więc ma postać 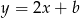 . Współczynnik
. Współczynnik 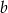 wyznaczmy podstawiając współrzędne punktu
wyznaczmy podstawiając współrzędne punktu 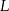
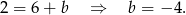
Zatem prosta ta ma równanie 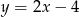 .
.
Teraz szukamy punktu wspólnego prostych 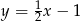 i
i 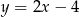 . Od razu porównujemy
. Od razu porównujemy 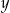 -ki.
-ki.
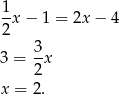
Zatem 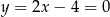 i
i 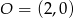 . Mamy stąd
. Mamy stąd
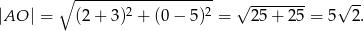
Sposób III
Zadanie możemy też rozwiązać zgadując z obrazka współrzędne punktu 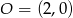 (co nie jest specjalnie trudne) i wykazując, że rzeczywiście jest to szukany punkt.
(co nie jest specjalnie trudne) i wykazując, że rzeczywiście jest to szukany punkt.
Aby wykazać, że punkt 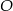 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 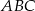 wystarczy pokazać, że odcinki
wystarczy pokazać, że odcinki 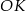 i
i 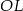 mają równe długości oraz, że są prostopadłe odpowiednio do prostych
mają równe długości oraz, że są prostopadłe odpowiednio do prostych 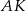 i
i 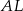 .
.
Zacznijmy od prostopadłości – zrobimy to sprawdzając, że iloczyny skalarne 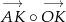 oraz
oraz 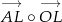 są równe 0. Liczymy
są równe 0. Liczymy
![−→ AK = [0 + 3,− 1 − 5] = [3,− 6] −→ −→ − → OK = [0 − 2,− 1 − 0] = [− 2,− 1] ⇒ AK ∘OK = − 6+ 6 = 0 −→ AL = [3 + 3,2 − 5] = [6,− 3] −O→L = [3− 2,2− 0] = [1,2] ⇒ −A→L ∘ −O→L = 6 − 6 = 0.](https://img.zadania.info/zad/2365104/HzadR83x.gif)
Pozostało sprawdzić, że 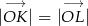 .
.
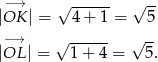
Zatem rzeczywiście punkt 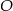 jest szukanym środkiem okręgu wpisanego w trójkąt
jest szukanym środkiem okręgu wpisanego w trójkąt  .
.
Długość odcinka 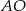 obliczamy jak w poprzednich sposobach.
obliczamy jak w poprzednich sposobach.
Sposób IV
Tym razem użyjemy więcej geometrii – zauważmy, że jeżeli 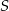 jest środkiem odcinka
jest środkiem odcinka 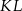 to trójkąty
to trójkąty 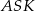 i
i 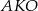 są podobne (oba są prostokątne i mają wspólny kąt przy wierzchołku
są podobne (oba są prostokątne i mają wspólny kąt przy wierzchołku 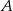 ). Mamy więc
). Mamy więc
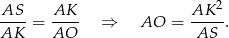
Długość odcinka 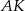 wyliczamy od razu
wyliczamy od razu
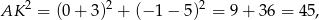
a długość odcinka 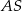 wyliczymy z twierdzenia Pitagorasa.
wyliczymy z twierdzenia Pitagorasa.
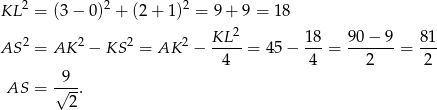
Mamy więc
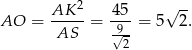
Odpowiedź: