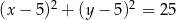Zadanie nr 2497898
Wyznacz równanie okręgu przechodzącego przez punkt 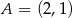 i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
i stycznego do obu osi układu współrzędnych. Rozważ wszystkie przypadki.
Rozwiązanie
Możemy rozpocząć od szkicowego rysunku. Łatwo spostrzec, że zdanie powinno mieć dwa rozwiązania.
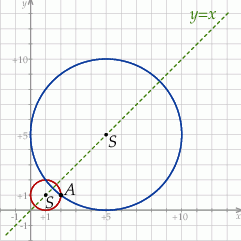
Jeżeli okrąg ma być styczny do obu osi układu, to jego środek musi leżeć na prostej 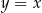 (druga możliwość, czyli środek leżący na prostej
(druga możliwość, czyli środek leżący na prostej 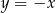 nie jest możliwa ze względu na położenie punktu
nie jest możliwa ze względu na położenie punktu 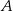 ). Oznaczmy więc współrzędne środka okręgu przez
). Oznaczmy więc współrzędne środka okręgu przez 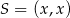 . Punkt ten musi być jednakowo odległy od osi i od punktu
. Punkt ten musi być jednakowo odległy od osi i od punktu 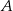 , co prowadzi do równania.
, co prowadzi do równania.
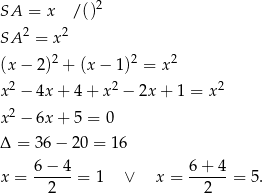
Otrzymaliśmy więc dwa okręgi spełniające warunki zadania
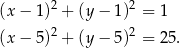
Odpowiedź: 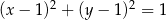 i
i