/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczny do prostej

Zadanie nr 3305371

Dodaj do ulubionych
Dodaj do rozwiązanych

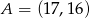Z punktu A = (1 7,16) poprowadzono styczne do okręgu o równaniu 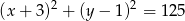(x + 3)2 + (y − 1)2 = 1 25 . Oblicz długość odcinka łączącego punkty styczności.

Rozwiązanie

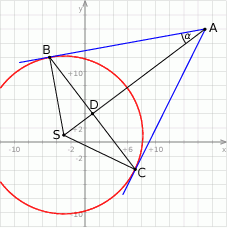
Dany okrąg to okrąg o środku 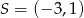S = (− 3,1) i promieniu 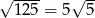√ ---- √ -- 1 25 = 5 5 . Możemy teraz wykonać szkicowy rysunek.

PIC

Obliczmy długości odcinków 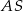AS i AB .

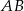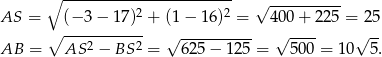
∘ ----------------------- √ ---------- AS = (− 3 − 17 )2 + (1 − 16 )2 = 400 + 225 = 25 ∘ ----------- √ ---------- √ ---- √ -- AB = AS 2 − BS2 = 625− 125 = 5 00 = 10 5 .

Sposób I

Zauważmy, że odcinek 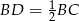BD = 12BC jest wysokością w trójkącie prostokątnym 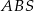ABS . Możemy więc obliczyć jego długość porównując dwa wzory na pole trójkąta ABS .

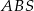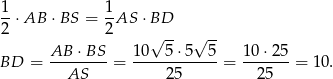
1- 1- 2 ⋅AB ⋅BS = 2 AS ⋅ BD √ -- √ -- BD = AB--⋅BS- = 10---5⋅5---5 = 1-0⋅25-= 10. AS 25 25

Zatem 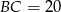BC = 20 .

Sposób II

Jeżeli oznaczmy 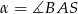α = ∡BAS to

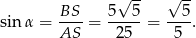
√ -- √ -- BS-- 5---5 --5- sin α = AS = 2 5 = 5 .

Z drugiej strony.

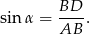
sin α = BD--. AB

Zatem

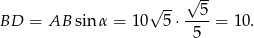
√ -- BD = AB sin α = 10√ 5-⋅--5-= 10. 5

Stąd 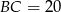BC = 20 .

Sposób III

Długość odcinka 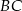BC możemy obliczyć korzystając z twierdzenia cosinusów. Musimy jednak najpierw obliczyć 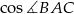co s∡BAC . Korzystając ze wzoru na 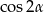cos2α mamy

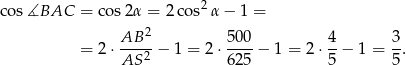
co s∡BAC = cos2α = 2co s2α − 1 = 2 = 2⋅ AB---− 1 = 2 ⋅ 50-0− 1 = 2 ⋅ 4-− 1 = 3. AS 2 62 5 5 5

Pozostało zastosować twierdzenie cosinusów.

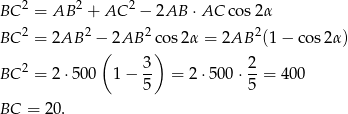
BC 2 = AB 2 + AC 2 − 2AB ⋅ AC co s2α BC 2 = 2AB 2 − 2AB 2co s2α = 2AB 2(1− cos2 α) ( 3) 2 BC 2 = 2 ⋅500 1− -- = 2 ⋅500 ⋅--= 400 5 5 BC = 20 .

 
Odpowiedź: 20

Wersja PDF