/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczny do prostej

Zadanie nr 4799177

Do okręgu należy punkt 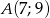A (7;9 ) , oraz jest on styczny do osi 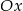Ox w punkcie 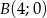B (4;0) . Podaj równanie tego okręgu.

Wersja PDF

Rozwiązanie

Zaczynamy od rysunku.

PIC

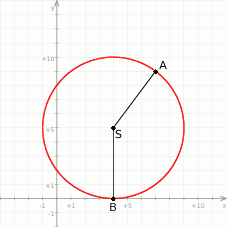
Skoro okrąg ma być styczny do osi 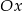Ox w punkcie 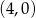(4,0 ) , jego środek musi leżeć na prostej 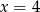x = 4 (bo środek leży na prostej prostopadłej do stycznej i przechodzącej przez punkt styczności). Szukamy zatem na tej prostej punktu 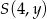S(4,y) , który jest równo odległy od punktów 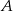A i B .

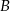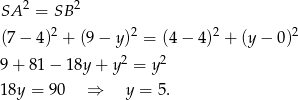
2 2 SA = SB (7− 4 )2 + (9 − y)2 = (4− 4 )2 + (y − 0)2 2 2 9+ 8 1− 18y+ y = y 18y = 90 ⇒ y = 5.

Zatem okrąg ma środek 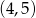(4,5) i promień 5, czyli ma równanie

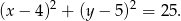
2 2 (x − 4) + (y − 5) = 25.

 
Odpowiedź: 2 2 (x − 4) + (y − 5) = 25

Wersja PDF