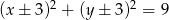/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczny do prostej

Zadanie nr 6904759

Dodaj do ulubionych
Dodaj do rozwiązanych

Napisz równanie okręgu o promieniu 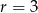r = 3 , stycznego do obu osi układu.

Rozwiązanie

Zaczynamy od rysunku.

PIC

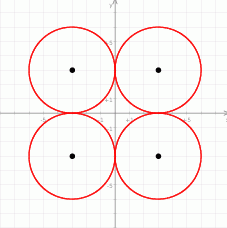
Skoro okrąg ma być styczny do obu osi układu, odległość jego środka od obu osi musi być równa 3. Zatem współrzędne środka są postaci 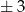± 3 . Są cztery takie punkty, co daje nam cztery okręgi.

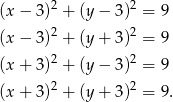
(x − 3)2 + (y − 3)2 = 9 2 2 (x − 3) + (y + 3) = 9 (x + 3)2 + (y − 3)2 = 9 (x + 3)2 + (y + 3)2 = 9.

 
Odpowiedź: (x ± 3)2 + (y ± 3)2 = 9

Wersja PDF