/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczny do prostej

Zadanie nr 7236411

Dodaj do ulubionych
Dodaj do rozwiązanych

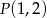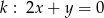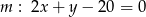Znajdź równanie okręgu przechodzącego przez punkt P(1,2) i stycznego jednocześnie do prostych k : 2x + y = 0 i m : 2x + y − 20 = 0 .

Rozwiązanie

Najpierw narysujmy szkicowy rysunek – widać z niego, że będą dwa takie okręgi.

PIC

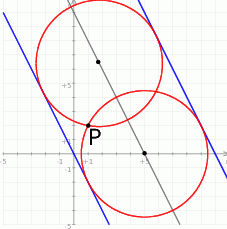
Ponieważ podane proste są równoległe, środek szukanego okręgu musi leżeć na prostej, która jest od nich równo odległa, czyli na prostej 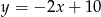y = − 2x+ 10 (prosta ta musi przecinać oś 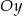Oy w połowie odcinka odciętego przez dwie podane proste, czyli w punkcie 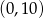(0,1 0) ). Środek okręgu jest więc postaci 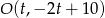O (t,− 2t+ 10) . Aby ustalić jaki jest promień szukanego okręgu, musimy obliczyć odległość między podanymi prostymi. W tym celu wybieramy na pierwszej z nich dowolny punkt, np. 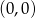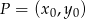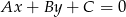(0,0) i podstawiamy do wzoru na odległość punktu P = (x ,y ) 0 0 od prostej Ax + By + C = 0 :

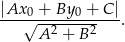
|Ax 0 + By 0 + C| ---√------------. A 2 + B 2

W naszej sytuacji mamy

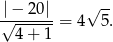
|− 20| √ -- √-------= 4 5. 4 + 1

Promień szukanego okręgu jest równy połowie tej odległości, czyli 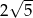√ -- 2 5 . Pozostało sprawdzić, kiedy okrąg

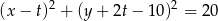
(x − t)2 + (y+ 2t− 10 )2 = 20

przechodzi przez punkt 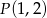P(1,2) . Podstawiamy współrzędne tego punktu do równania okręgu.

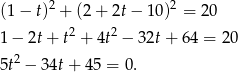
2 2 (1− t) + (2 + 2t− 10) = 20 1− 2t+ t2 + 4t2 − 32t+ 64 = 20 2 5t − 3 4t+ 45 = 0.

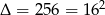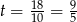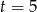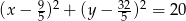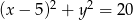Dalej Δ = 2 56 = 162 , t = 1180 = 95 lub t = 5 . Daje to nam dwa okręgi (x − 9)2 + (y − 32)2 = 20 5 5 i (x − 5)2 + y2 = 20 .  
Odpowiedź: 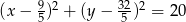9 2 32 2 (x − 5) + (y − 5 ) = 2 0 lub (x − 5)2 + y2 = 2 0

Wersja PDF