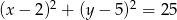/Szkoła średnia/Geometria/Geometria analityczna/Okrąg/Styczny do prostej

Zadanie nr 7272824

Dodaj do ulubionych
Dodaj do rozwiązanych

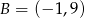Punkt B = (− 1,9) należy do okręgu stycznego do osi 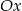Ox w punkcie 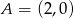A = (2,0) . Wyznacz równanie tego okręgu.

Rozwiązanie

Rozpoczynamy od naszkicowania sobie o co chodzi.

PIC

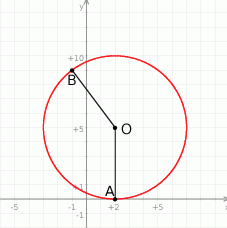
Ponieważ okrąg jest styczny od osi 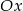Ox w punkcie 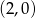(2,0 ) , jego środek musi leżeć na prostej 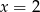x = 2 , czyli jest postaci 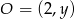O = (2,y) dla pewnego 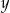y . Z drugiej strony ten środek musi być równo odległy od obydwu podanych punktów, co daje równanie (od razu porównujemy kwadraty odległości)

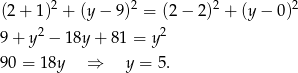
2 2 2 2 (2+ 1 ) + (y − 9) = (2− 2 ) + (y − 0) 9+ y 2 − 1 8y+ 81 = y2 90 = 18y ⇒ y = 5.

Zatem promień okręgu jest równy 5 i okrąg ma równanie

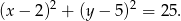
2 2 (x − 2) + (y − 5) = 25.

 
Odpowiedź: (x − 2)2 + (y − 5)2 = 25

Wersja PDF