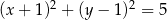Zadanie nr 7820974
Okrąg  ma środek
ma środek 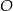 i jest styczny prostej
i jest styczny prostej 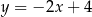 w punkcie
w punkcie 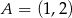 . Wyznacz równanie okręgu
. Wyznacz równanie okręgu  , jeżeli
, jeżeli ![−→ OA = [2,1]](https://img.zadania.info/zad/7820974/HzadT5x.gif) .
.
Rozwiązanie
Szkicujemy opisaną sytuację.
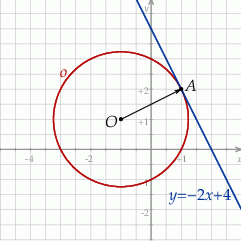
Z danego wektora 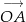 obliczamy współrzędne punktu
obliczamy współrzędne punktu 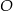 .
.
![−→ [2,1] = OA = A − O ⇒ O = (1,2) − [2,1] = (− 1,1).](https://img.zadania.info/zad/7820974/HzadR3x.gif)
Musimy jeszcze wyznaczyć promień okręgu. Możemy to zrobić na różne sposoby: jako odległość punktu 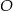 od danej stycznej, jako długość odcinka
od danej stycznej, jako długość odcinka 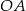 lub jako długość wektora
lub jako długość wektora 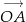 . My zrobimy to tym ostatnim sposobem.
. My zrobimy to tym ostatnim sposobem.
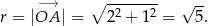
Okrąg  ma więc równanie
ma więc równanie
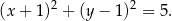
Odpowiedź: