Zadanie nr 9708243
Do okręgów o równaniach 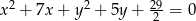 i
i 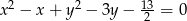 poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
poprowadzono wspólną styczną. Oblicz długość odcinka łączącego punkty styczności. Rozważ wszystkie możliwości.
Rozwiązanie
Aby narysować opisaną sytuację przekształcamy podane równania okręgu tak, aby było widać jakie mają środki i promienie. Pierwszy okrąg
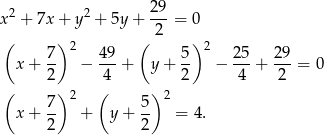
Jest to więc okrąg o środku 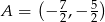 i promieniu 2.
i promieniu 2.
Teraz drugi okrąg
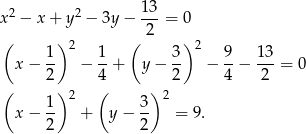
Jest to więc okrąg o środku 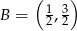 i promieniu 3. Szkicujemy teraz obrazek.
i promieniu 3. Szkicujemy teraz obrazek.
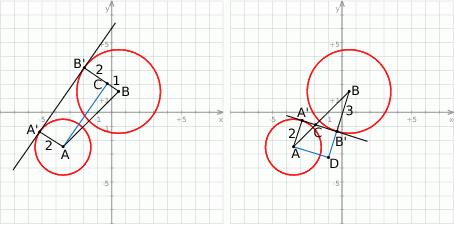
Z rysunku widać, że są dwa rodzaje stycznych. Zajmiemy każdą z tych dwóch możliwych sytuacji z osobna.
Jeżeli okręgi leżą po jednej stronie stycznej (sytuacja z lewego rysunku) to odległość 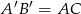 możemy obliczyć z trójkąta prostokątnego
możemy obliczyć z trójkąta prostokątnego 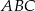 . Aby móc to zrobić obliczmy najpierw odległość między środkami okręgów.
. Aby móc to zrobić obliczmy najpierw odległość między środkami okręgów.
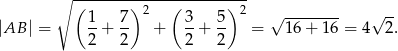
Obliczamy teraz długość odcinka 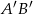 .
.
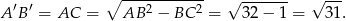
Zajmijmy się teraz drugą sytuacją, gdy okręgi leżą po dwóch różnych stronach stycznej.
Sposób I
Zauważmy, że trójkąty 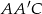 i
i 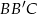 są prostokątne i mają kąt wspólny przy wierzchołku
są prostokątne i mają kąt wspólny przy wierzchołku 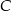 . Są więc podobne i mamy
. Są więc podobne i mamy 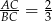 . To pozwala nam obliczyć długości odcinków
. To pozwala nam obliczyć długości odcinków 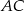 i
i 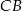 . Wiemy już, że
. Wiemy już, że 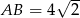 , więc
, więc
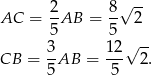
Teraz możemy już łatwo obliczyć długości odcinków 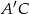 i
i 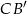 .
.
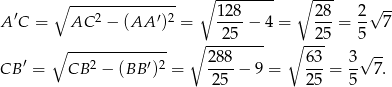
W takim razie
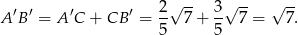
Sposób II
Tym razem na prawym rysunku prowadzimy przez punkt 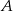 prostą równoległą do stycznej oraz zaznaczamy jej punkt wspólny
prostą równoległą do stycznej oraz zaznaczamy jej punkt wspólny 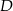 z prostą
z prostą 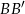 . Otrzymujemy w ten sposób trójkąt prostokątny
. Otrzymujemy w ten sposób trójkąt prostokątny 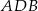 , w którym
, w którym
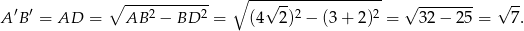
Odpowiedź: 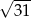 lub
lub