Zadanie nr 9797596
Wiadomo, że okrąg jest styczny do prostej o równaniu 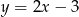 w punkcie
w punkcie 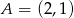 i styczny do prostej o równaniu
i styczny do prostej o równaniu 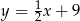 w punkcie
w punkcie 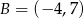 . Oblicz promień tego okręgu.
. Oblicz promień tego okręgu.
Rozwiązanie
Zacznijmy od schematycznego rysunku.
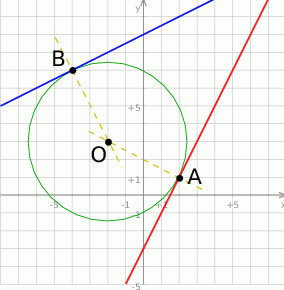
Jak zwykle w przypadku zadania z geometrii analitycznej jest wiele sposobów rozwiązania. My pokażemy dwa z nich.
Sposób I
Spróbujemy znaleźć współrzędne środka 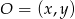 okręgu, o którym mowa w treści zadania. W tym celu napiszemy równania prostych prostopadłych do podanych prostych w punktach styczności z okręgiem i znajdziemy ich punkt wspólny. Prosta prostopadła do
okręgu, o którym mowa w treści zadania. W tym celu napiszemy równania prostych prostopadłych do podanych prostych w punktach styczności z okręgiem i znajdziemy ich punkt wspólny. Prosta prostopadła do 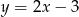 jest postaci
jest postaci 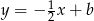 . Ponadto szukamy prostej przechodzącej przez punkt
. Ponadto szukamy prostej przechodzącej przez punkt 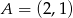 , czyli
, czyli
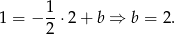
Podobnie znajdujemy drugą prostą. Ma on postać 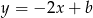 oraz
oraz
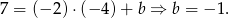
Aby wyznaczyć 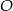 , musimy znaleźć punkt wspólny tych dwóch prostych
, musimy znaleźć punkt wspólny tych dwóch prostych
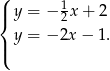
Odejmując od pierwszego równania drugie (żeby skrócić 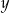 ), otrzymujemy
), otrzymujemy
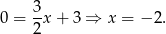
Zatem 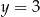 i
i 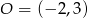 .
.
Pozostało wyliczyć promień okręgu, czyli długość odcinka 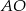 :
:
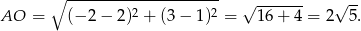
Sposób II
Podobnie jak poprzednio, znajdziemy współrzędne punktu 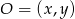 . Jakie ten punkt ma własności? Po pierwsze jest równoodległy od podanych prostych. Jak to zapisać? – trzeba skorzystać ze wzoru na odległość punktu
. Jakie ten punkt ma własności? Po pierwsze jest równoodległy od podanych prostych. Jak to zapisać? – trzeba skorzystać ze wzoru na odległość punktu 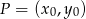 od prostej
od prostej 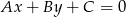 .
.
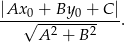
Żeby nie mieć ułamków, równanie drugiej prostej zamieńmy na 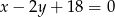 i mamy wtedy:
i mamy wtedy:
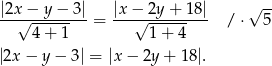
Jak teraz opuścić wartości bezwględne? Do tego potrzebna jest informacja o położeniu punktu 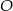 względem danych prostych. Dla punktu na prostej wyrażenie, które znajduje się pod wartością bezwzględną jest 0. Jeżeli punkt jest na lewo od prostej, to ma
względem danych prostych. Dla punktu na prostej wyrażenie, które znajduje się pod wartością bezwzględną jest 0. Jeżeli punkt jest na lewo od prostej, to ma  -a mniejszego, czyli wyrażenie jest ujemne. Gdy jest na prawo, to
-a mniejszego, czyli wyrażenie jest ujemne. Gdy jest na prawo, to  jest większy, więc jest dodatnie. Nasz punkt
jest większy, więc jest dodatnie. Nasz punkt 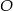 jest na prawo od pierwszej prostej i na lewo od drugiej, zatem
jest na prawo od pierwszej prostej i na lewo od drugiej, zatem
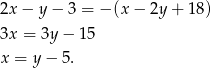
Dobrze, ale mamy jedno równanie a dwie niewiadome (nic w tym dziwnego, na razie wyliczyliśmy tylko równanie dwusiecznej podanego kąta). Drugie równanie to fakt, że odległość punktu 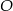 od danych prostych to ma być dokładnie jego odległosć od punktu
od danych prostych to ma być dokładnie jego odległosć od punktu 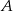 . Od razu porównamy kwadraty odległości i wykorzystamy poprzednie wyliczenie odległości
. Od razu porównamy kwadraty odległości i wykorzystamy poprzednie wyliczenie odległości 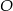 od pierwszej prostej
od pierwszej prostej
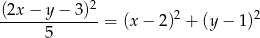
Zanim przkształcimy to dalej podstawmy wyliczone już 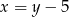
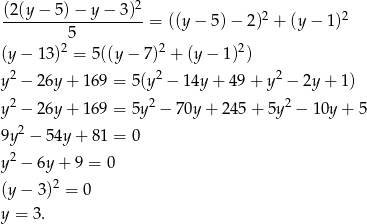
Tak więc 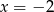 i promień wyliczamy jak w poprzednim sposobie.
i promień wyliczamy jak w poprzednim sposobie.

