Zadanie nr 1606521
Określ zbiór wartości i przedziały monotoniczności funkcji 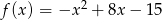 .
.
Rozwiązanie
Będziemy korzystać z tego, że funkcja kwadratowa 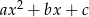 , gdzie
, gdzie 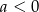 przyjmuje największą wartość w wierzchołku i jest rosnąca na lewo oraz malejąca na prawo od wierzchołka.
przyjmuje największą wartość w wierzchołku i jest rosnąca na lewo oraz malejąca na prawo od wierzchołka.
Zapiszmy funkcję w postaci kanonicznej
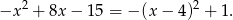
Wierzchołek paraboli jest w punkcie 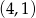 , czyli zbiór wartości to
, czyli zbiór wartości to 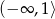 . Funkcja jest rosnąca dla
. Funkcja jest rosnąca dla 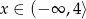 i malejąca dla
i malejąca dla 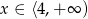 . Na koniec obrazek
. Na koniec obrazek
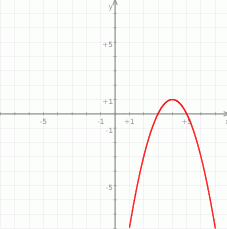
Odpowiedź: Zbiór wartości: 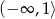 , rosnąca na
, rosnąca na 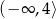 , malejąca na
, malejąca na